极限

[“极限”是数学中的分支——微积分的基础概念，广义的“极限”是指“无限靠近而永远不能到达”的意思。数学中的“极限”指：某一个函数中的某一个变量，此变量在变大（或者变小）的永远变化的过程中，逐渐向某一个确定的数值A不断地逼近而“永远不能够重合到A”（“永远不能够等于A，但是取等于A‘已经足够取得高精度计算结果）的过程中，此变量的变化，被人为规定为“永远靠近而不停止”、其有一个“不断地极为靠近A点的趋势”。极限是一种“变化状态”的描述。此变量永远趋近的值A叫做“极限值”（当然也可以用其他符号表示）。

证明：1=0.9999·····？

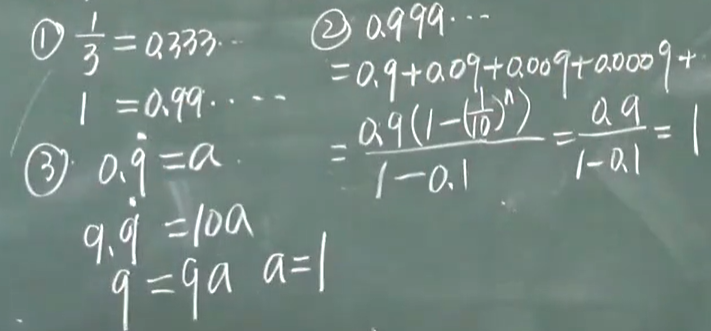
比如

假设有一圆

有内接圆面积$A_1$

记内接十二边形的面积为$A_2$

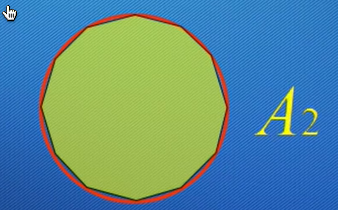
24边形

就可以得到一个数列{$A_n$}

数列的极限

当n→$\infty$时，{$A_n$}也无限接近于某一确定的数值，这个数值称为数列{$A_n$}当n→$\infty$时的极限。

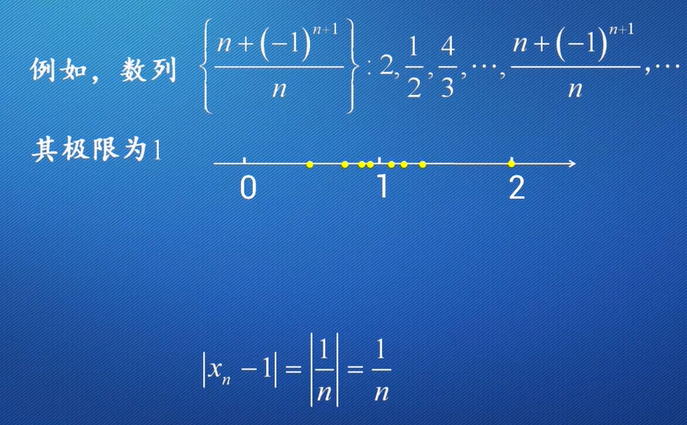
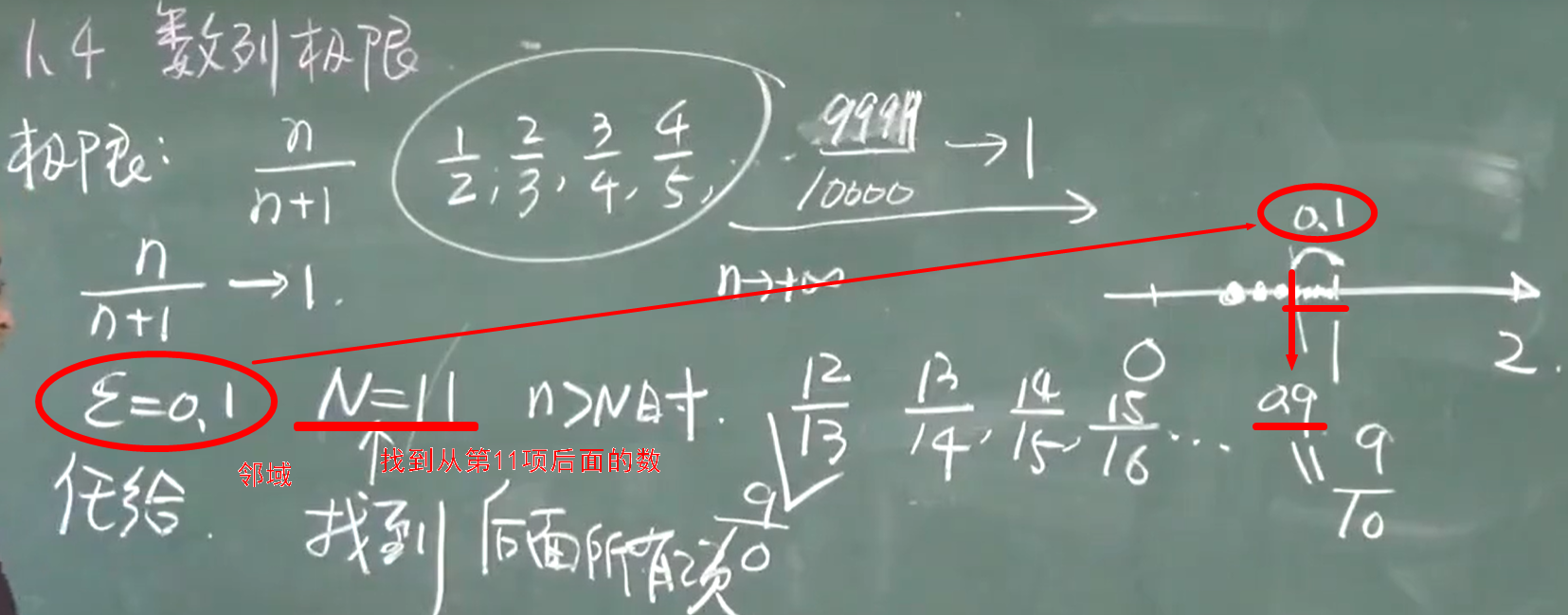
后面的值都落在这个邻域里面

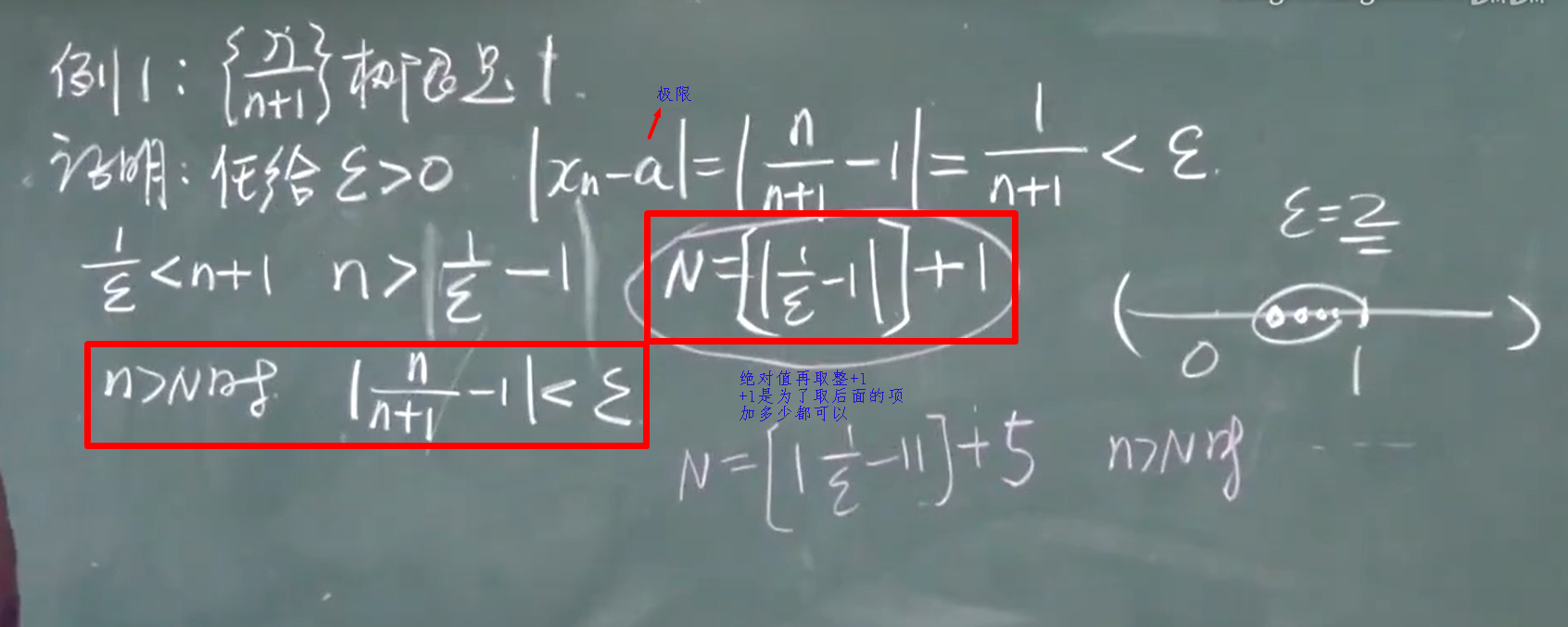
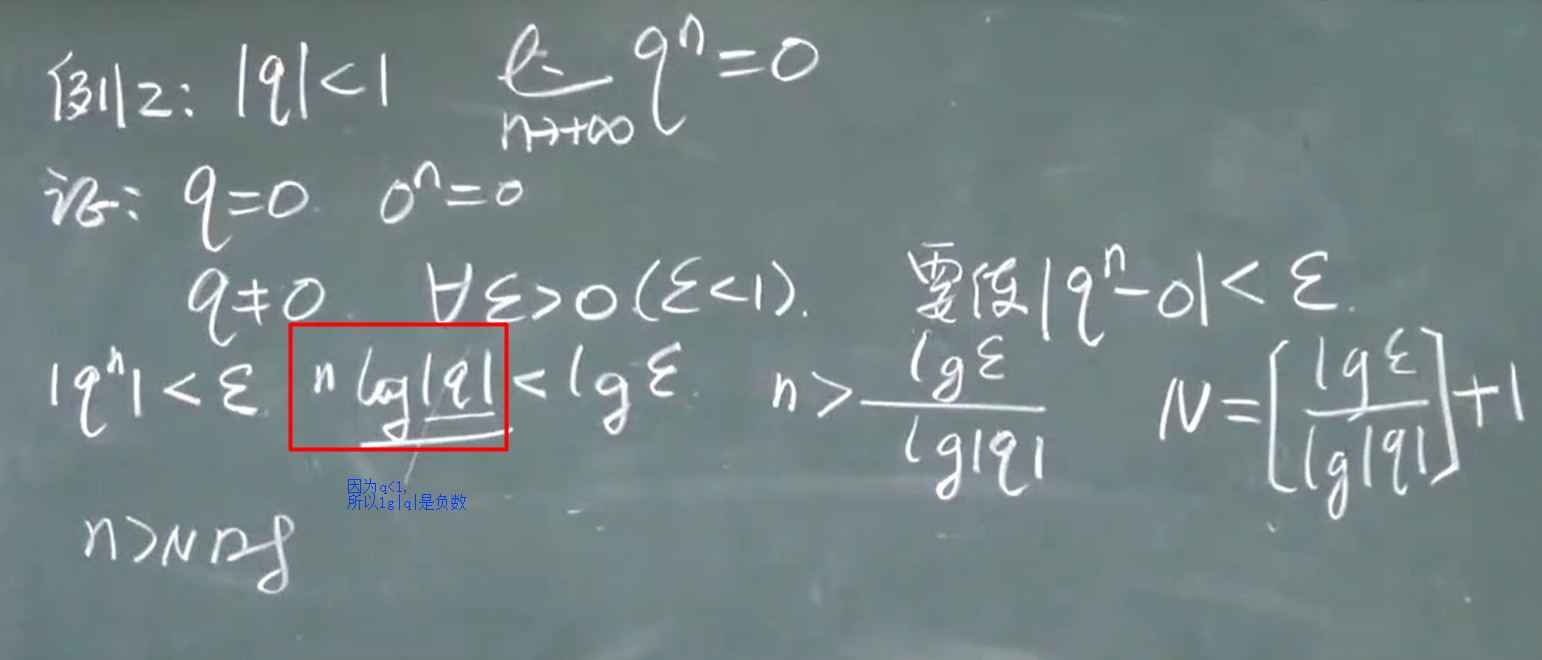
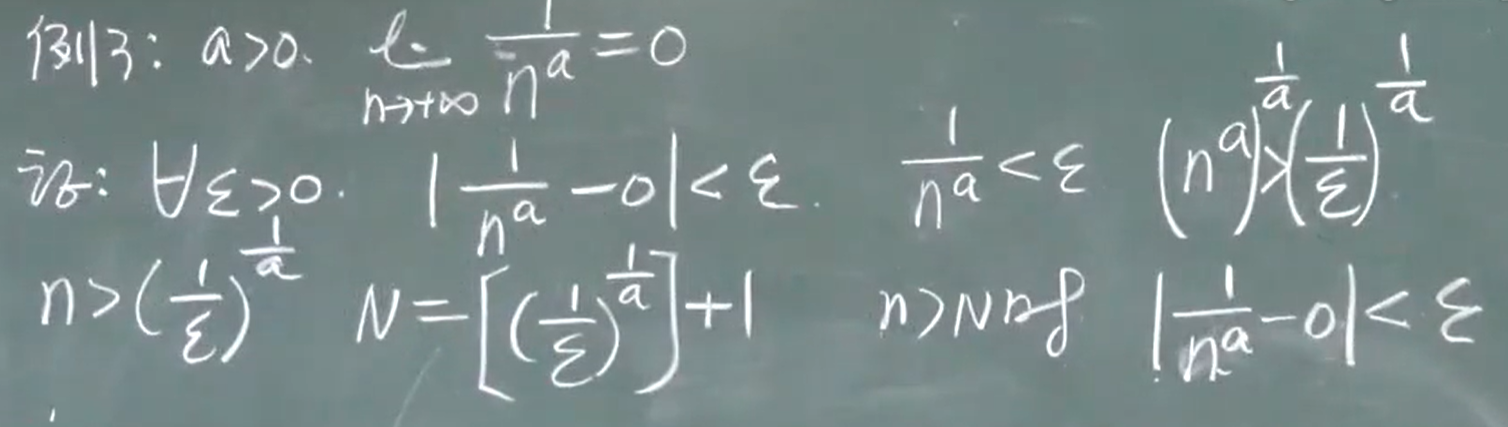
n一定是 > ???

要求 $\lvert x_n -1 \rvert$=$\frac{1}{n}$<$\epsilon$,只要n>[$\frac{1}{\epsilon} $],以后的一切项均满足 $\lvert x_n -1 \rvert$<$\epsilon$.

对于任意给定的正数$\epsilon$，总存在着一个正整数N(比如取N=[$\frac{1}{\epsilon}$]),当n>N时，

$$\lvert x_n -1 \rvert<\epsilon$$

记作

$$\lim_{n\to \infty} x_n = a或x_n→a(n→\infty)$$

如果上述a不存在，则称数列 $${x_n}$$没有极限,或者说数列 $${x_n}$$ 是发散的，也说 $\lim_{n\to \infty} x_n$ 不存在.

注意：

1.$\epsilon$的“任意给定”性极其重要；

2.N与$\epsilon$有关，有$\epsilon$的给定而确定；

3.$\forall$表示“任意给定”，$\exists$表示“存在”

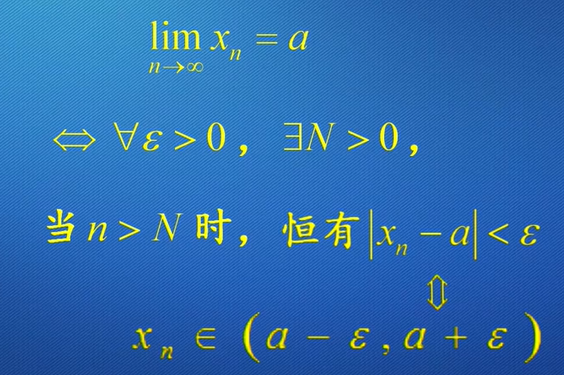
例子：

性质

性质1：{$x_n$}收敛 ，极限唯一.

性质2：{$x_n$}收敛 ，有界

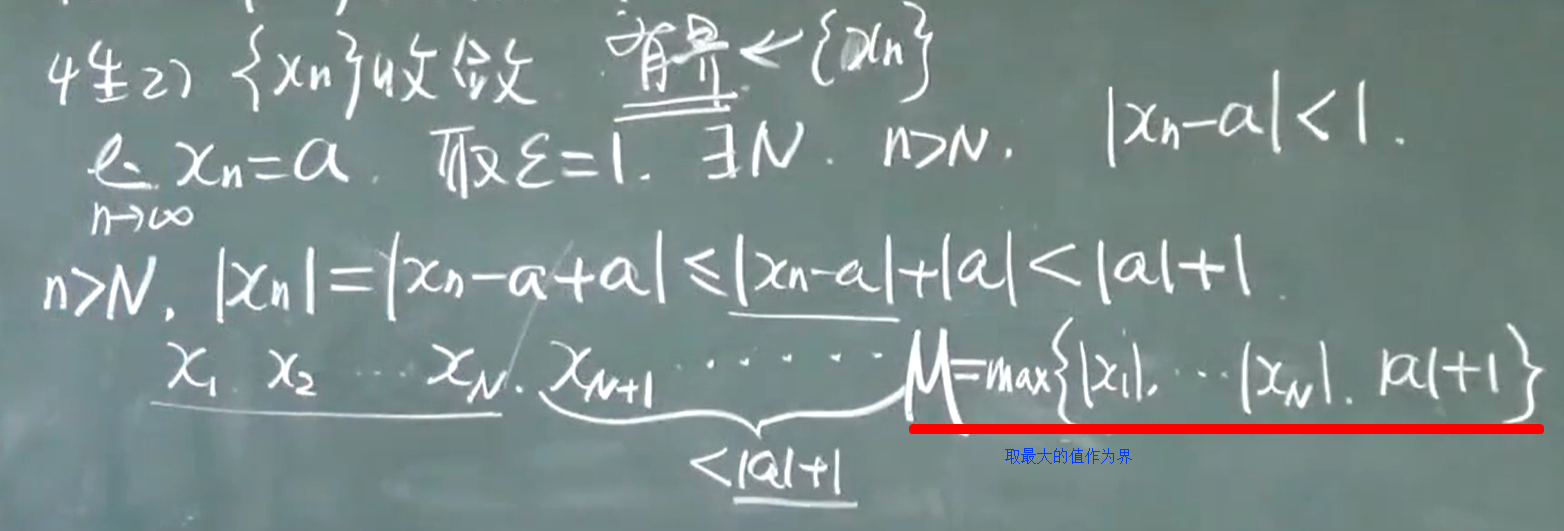
• 有界是收敛的必要，不是充分条件
• 单调有界，则有极限

性质3：保号性$\lim_{x_n} = a$ , a>0(a<0) ,$\exists$N, n>N ,$x_n$>0

性质4：{$x_n$}收敛于a，子数列{$x_kn$}收敛于a.

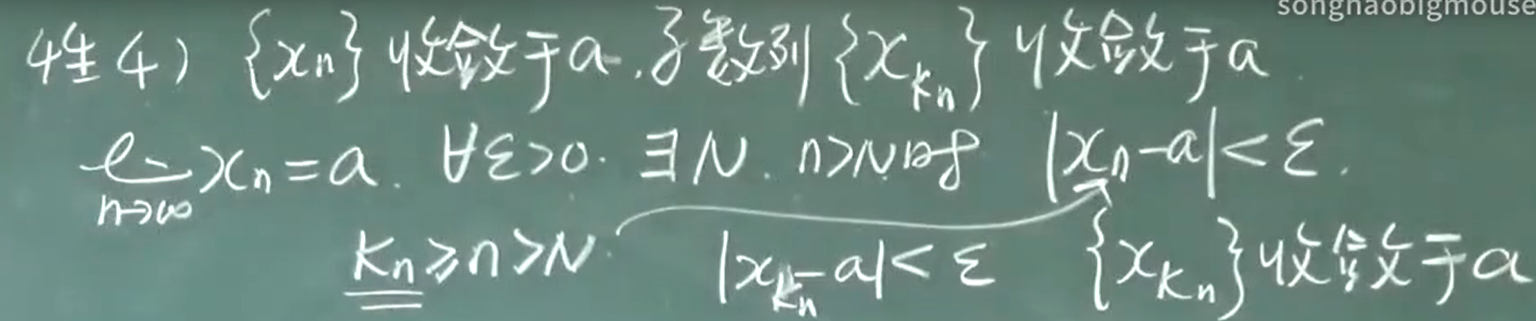
函数极限：

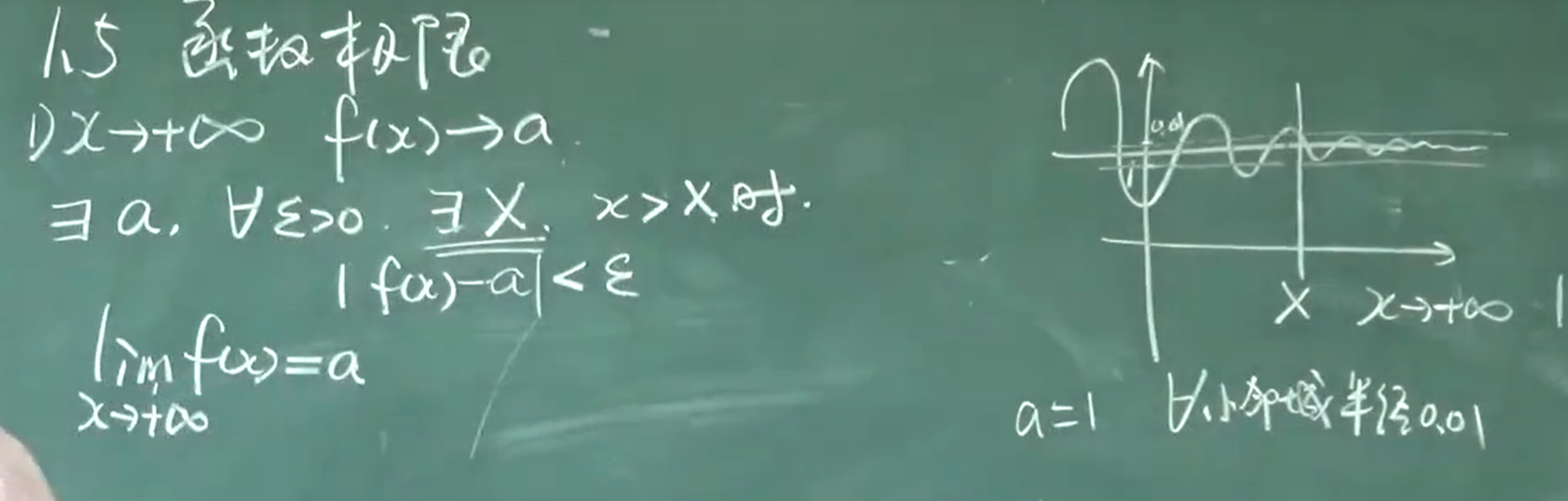
< $\epsilon$

取 X

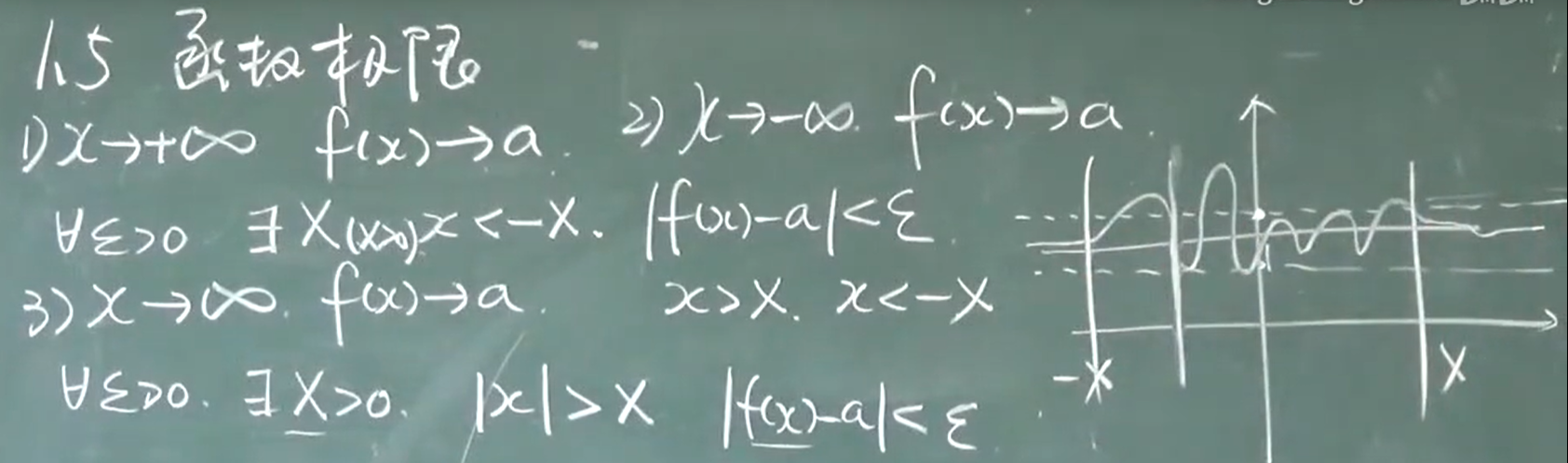
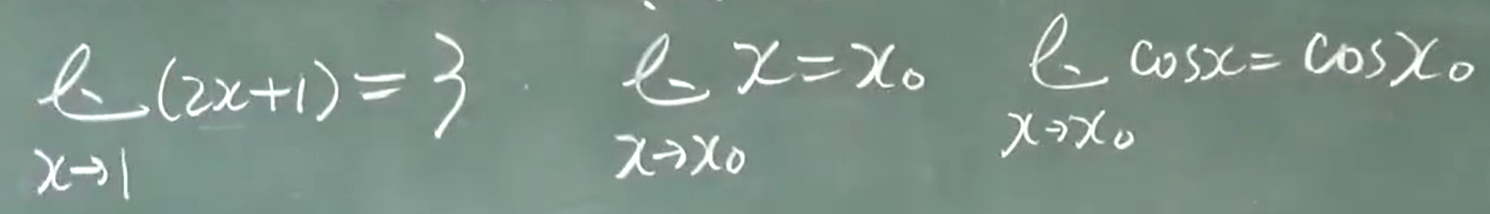
x→$x_0$时函数f(x)的极限

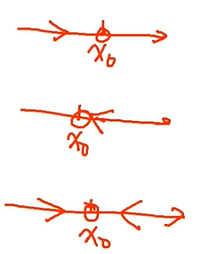
(1)x→$x_0^-$,表示x从点$x_0$的左侧无限接近于$x_0$,此时x<$x_0$;

(2)x→$x_0^+$,表示x从点$x_0$的右侧无限接近于$x_0$,此时x>$x_0$;

(3)x→$x_0$,表示x从点$x_0$的左右两侧无限接近于$x_0$.

注意：

(1)$x_0$是一个常数，而x是动点，是变化的量.

(2)在上述x的三个变化过程中，x无限地接近$x_0$,但永远不等于$x_0$.

左极限：

$$f(x_0^-)=\lim_{x\to x_0^-} f(x) = A$$

称函数f(x)当x→$x_0^-$时以A为极限，简称f(x)在$x_0$点处左极限为A；

右极限：

$$f(x_0^+)=\lim_{x\to x_0^+} f(x) = A$$

称函数f(x)当x→$x_0^+$时以A为极限，简称f(x)在$x_0$点处右极限为A；

极限：

$$\lim_{x\to x_0^-}f(x)=\lim_{x\to x_0^+}f(x)=\lim_{x\to x_0}f(x)=A$$

称函数f(x)当x→$x_0$时以A为极限，简称f(x)在$x_0$点处极限为A；

函数y=f(x)在$x_0$处的极限与$f(x_0)$的取值、是否存在毫无关系!

性质：

1.$\limf(x)$存在，是唯一的

2.局部有界性

3.局部保号性