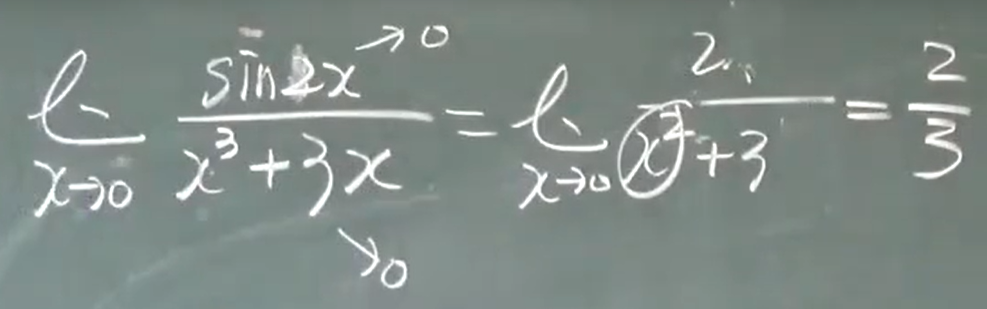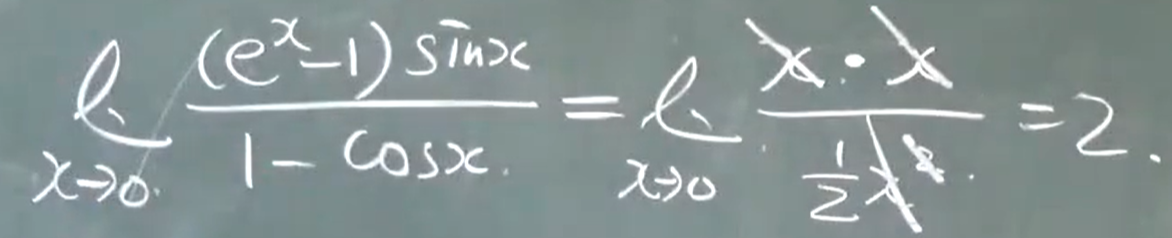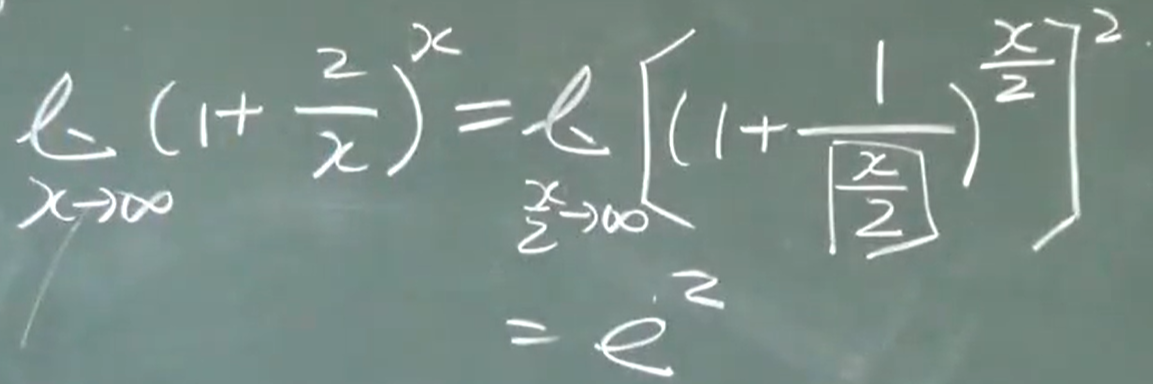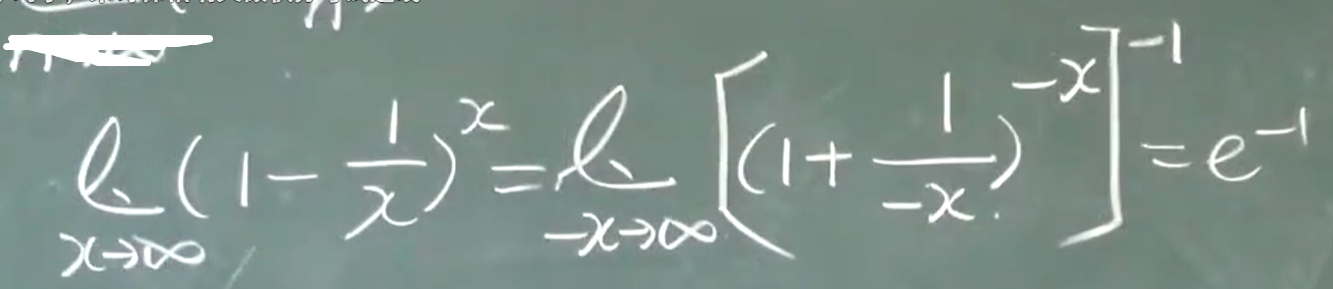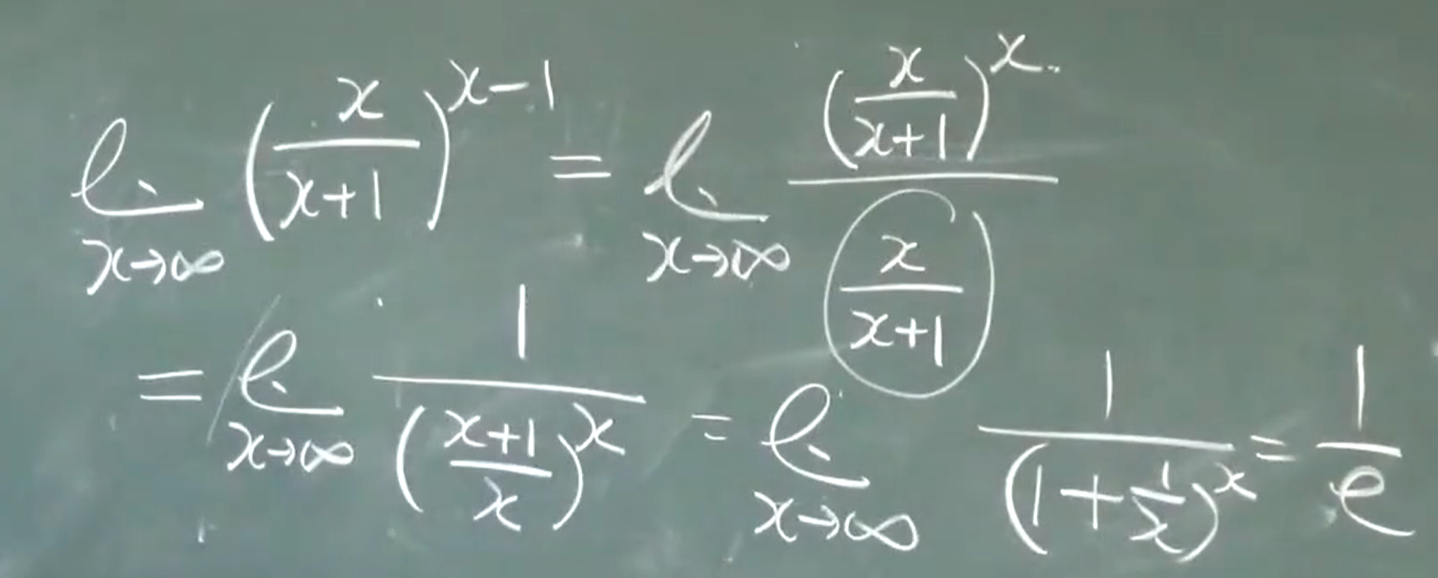无穷小量

定义：

极限为0的变量称为无穷小量，简称无穷小.

f(x)→0

常用希腊字母 $\alpha$ ,$\beta$ ,$\gamma$

$$\lim_{x\to0}x^2=0 极限为0$$

$$\lim_{x\to1}x^2=1 极限为1$$

$$\lim_{x\to\infty}x^2=0 极限为\infty$$

定理:

1.无穷小 × 有界 是无穷小

另一个例题

分解后面的ardtanx，加上绝对值|ardtanx|，说明是有界的。

2.

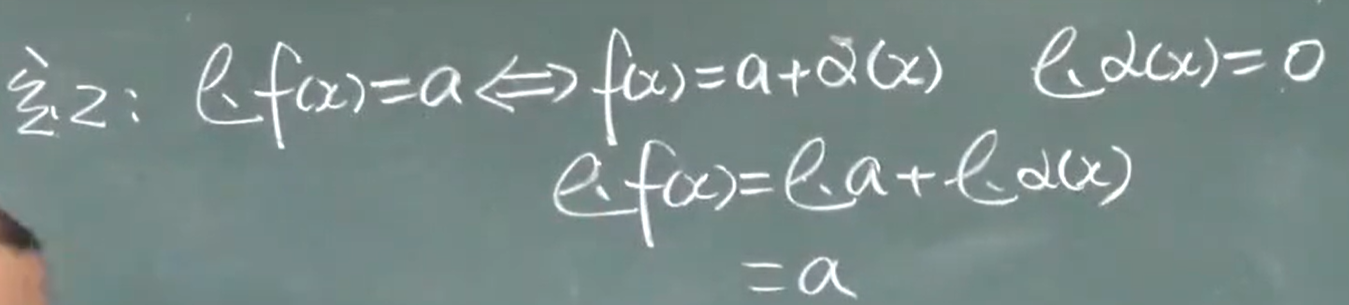
无穷大

$f(x)->+\infty 或-\infty$

1)两个无穷大相乘=无穷大

2)无穷大+有界->无穷大

定理：

• f(x)无穷大 $\frac{1}{f(x)}$无穷小 (同一变化过程)
• f(x)无穷小 $\frac{1}{f(x)}$无穷小(同一变化过程)

极限的运算法则

定理(四则运算) 若$\lim f(x)=a , \lim g(x)=b$（前提是每个函数极限存在,项是有限个的）

1)$\lim (f(x)+g(x))=\lim f(x) ± \lim g(x)=a ± b$

2)$\lim f(x)g(x)=\lim f(x) · \lim g(x)$

3)$\lim \frac{f(x)}{g(x)}=\frac {\lim f(x)}{\lim g(x)}(b≠0)$

其实就是把极限带进去

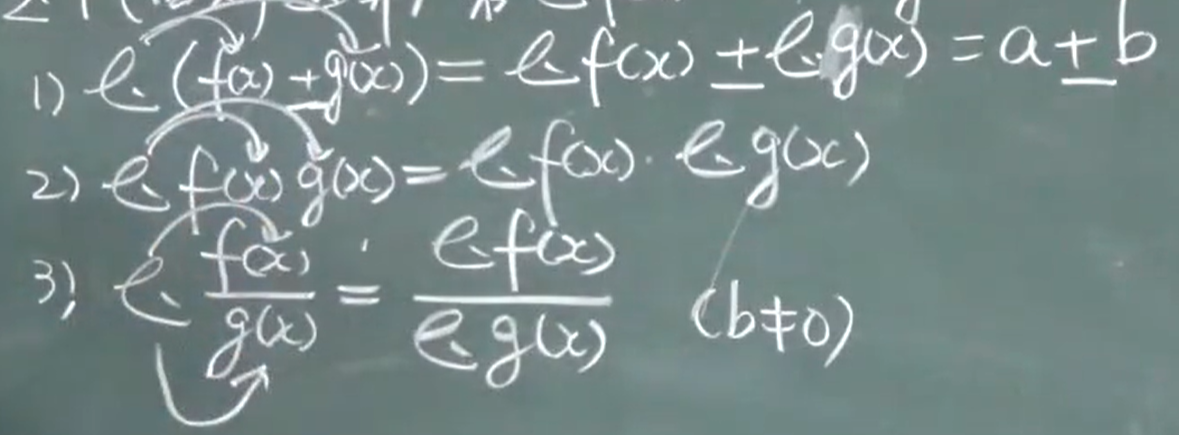
$\lim f(x)^n=(\lim f(x))^n$

例如：

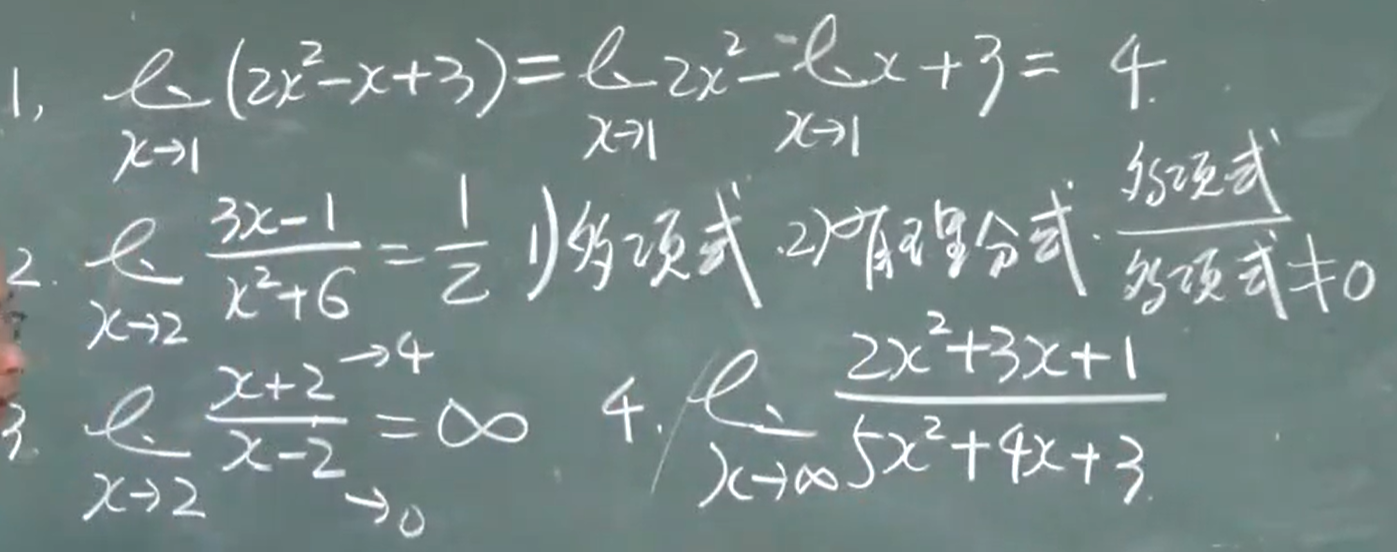
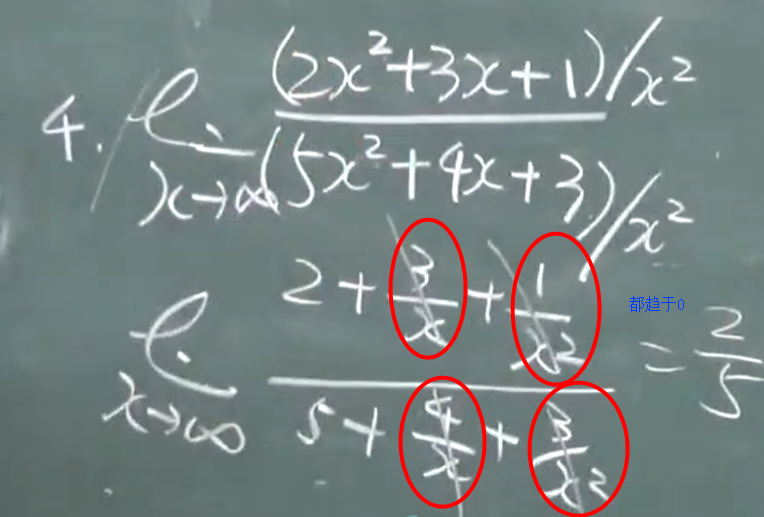
$\frac{\infty}{\infty}$

分子、分母同次，最高次的系数之比（分子分母都趋于无穷）

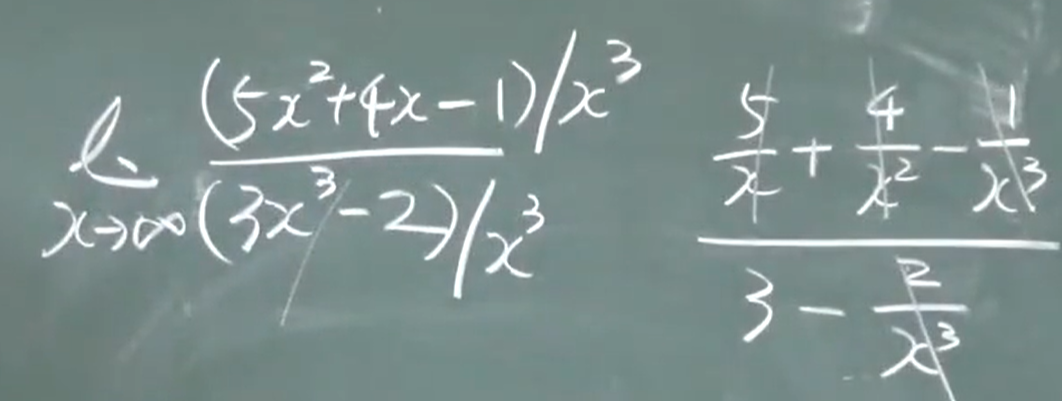
分母次数高，0

分子次数高，$\infty$

分子有理化

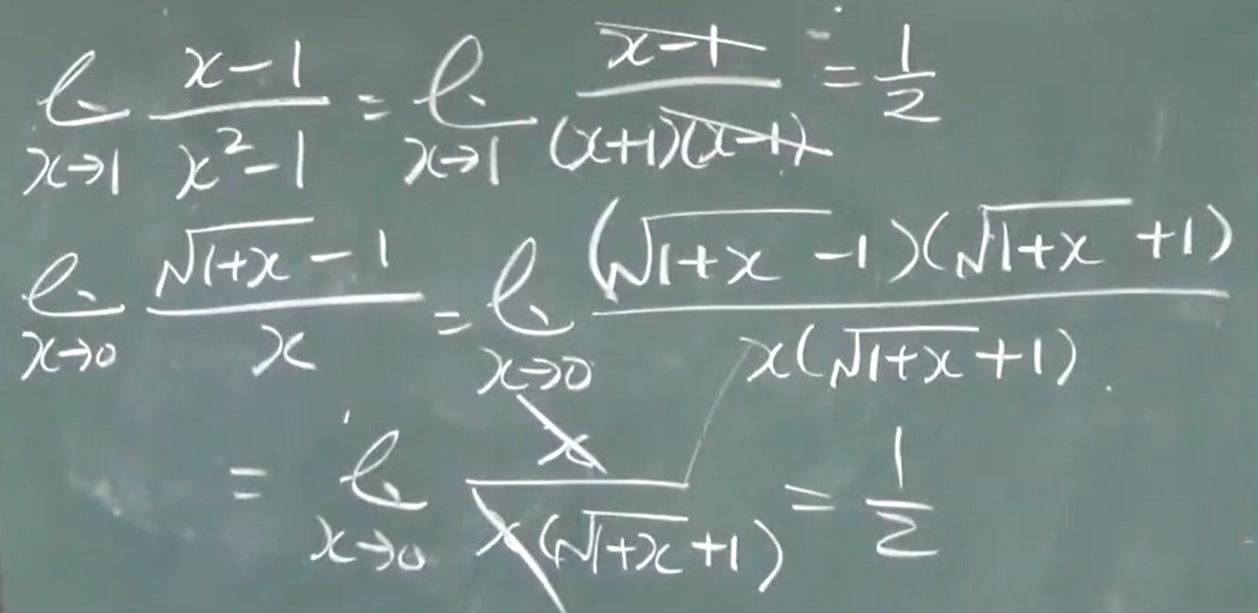
无限个项：多项式

$ \frac{n(a_1+a_n)}{2}$

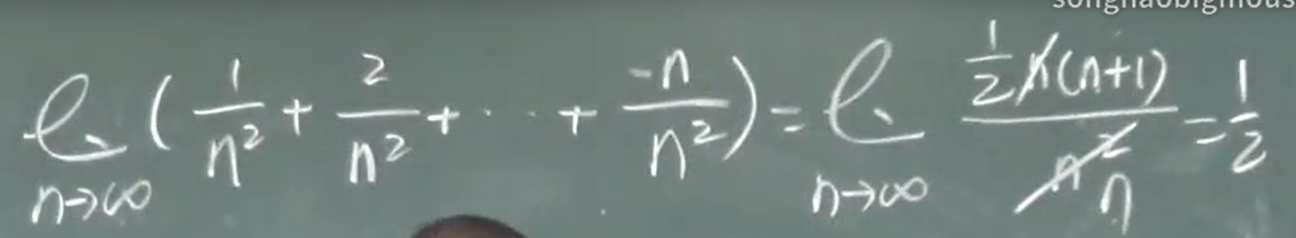
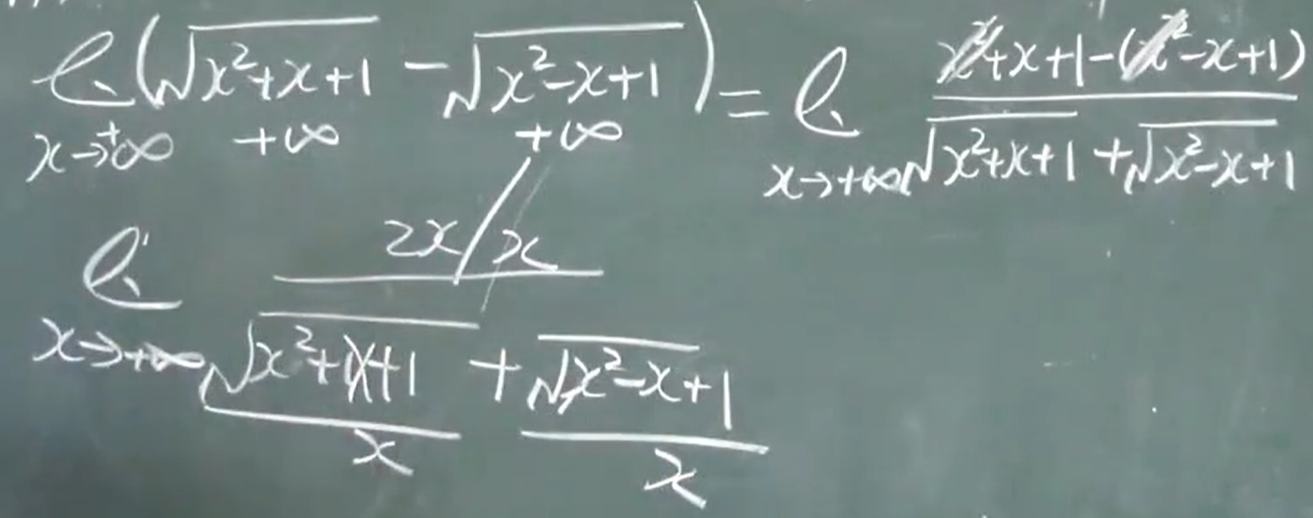
=1

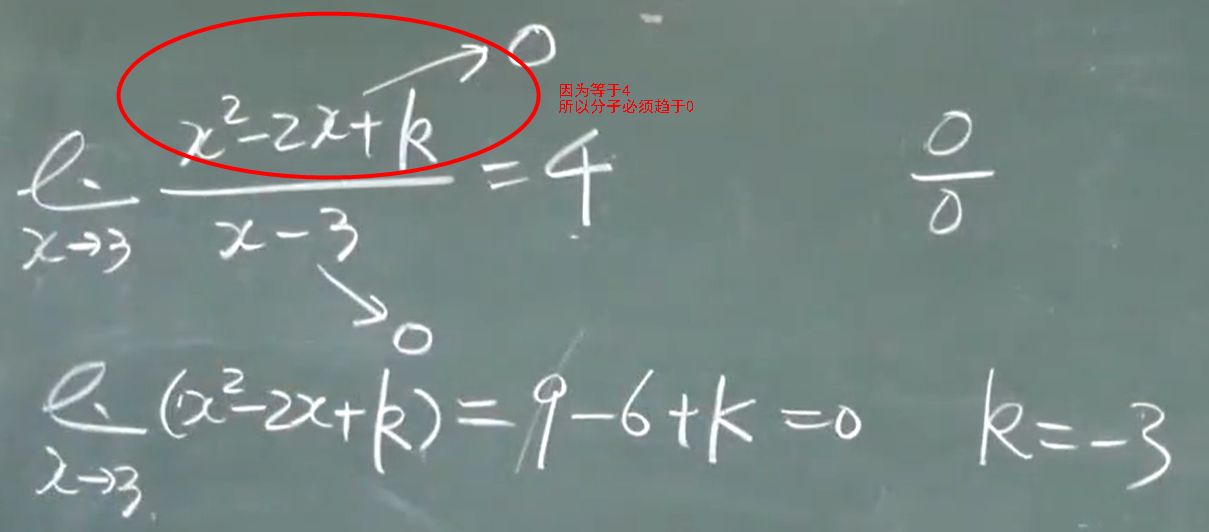
极限存在准则 两个重要极限

一、夹逼定理：存在三个函数f(x).g(x).h(x)

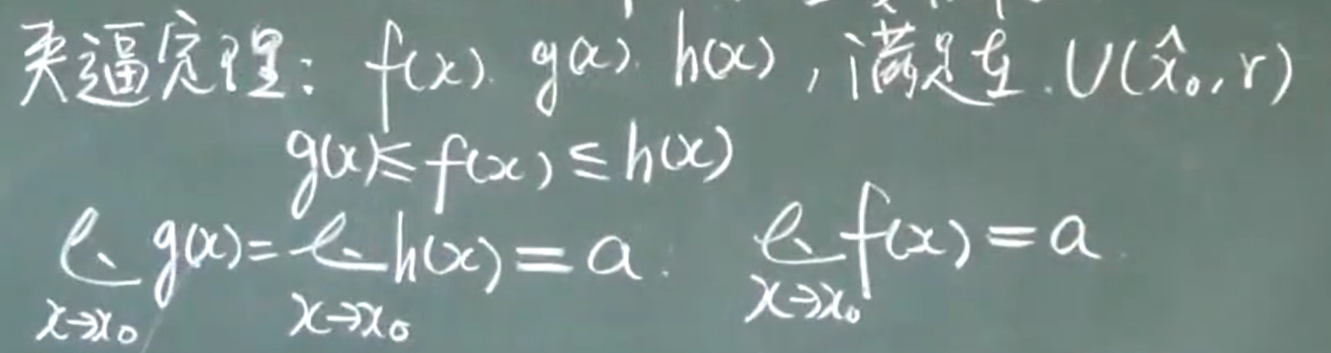
中间的一堆乘起来小于1，当n趋于无穷时，左边趋于0，右边趋于0

二、单调有界数列必有极限

∴单调递增

两个重要极限

$$\lim_{x\to0} \frac{sinx}{x}=1$$

例题1

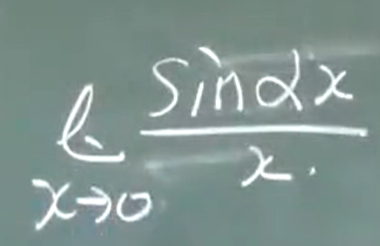
例题2

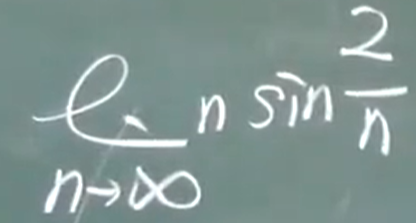
例题3

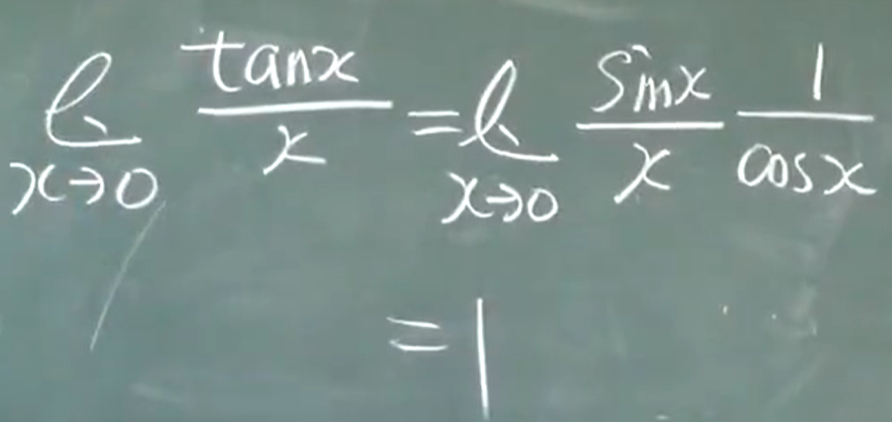
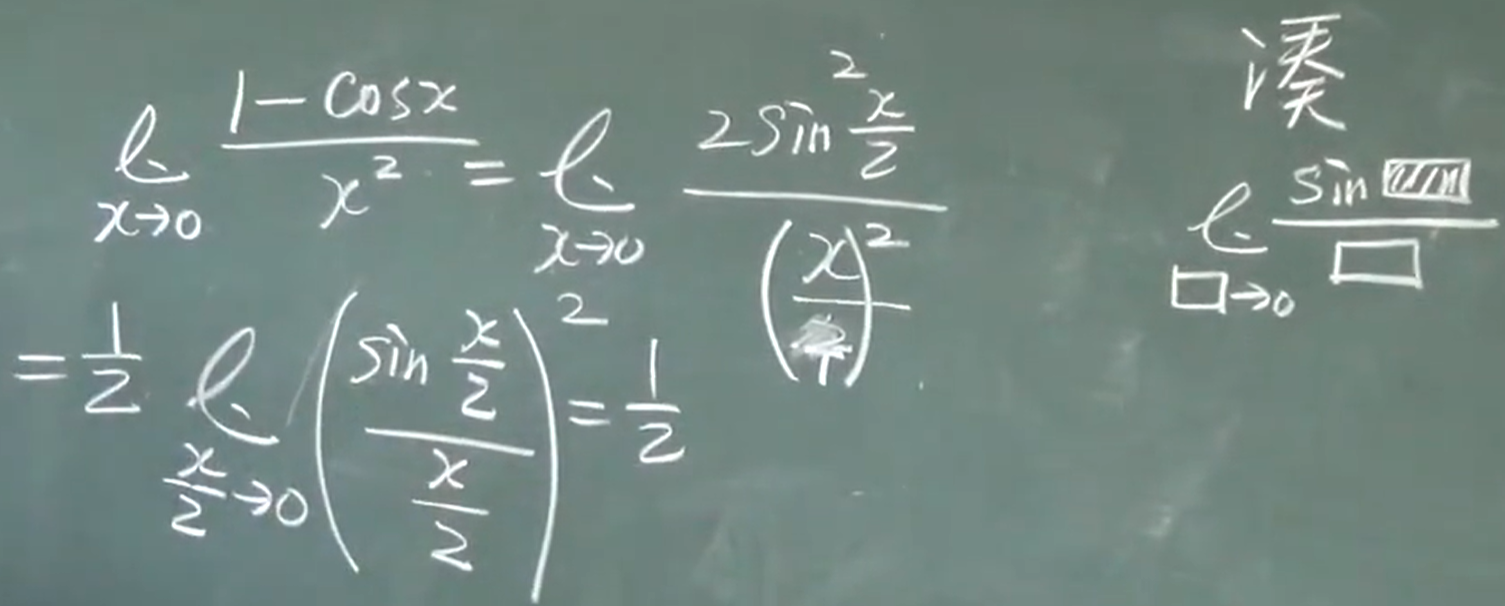
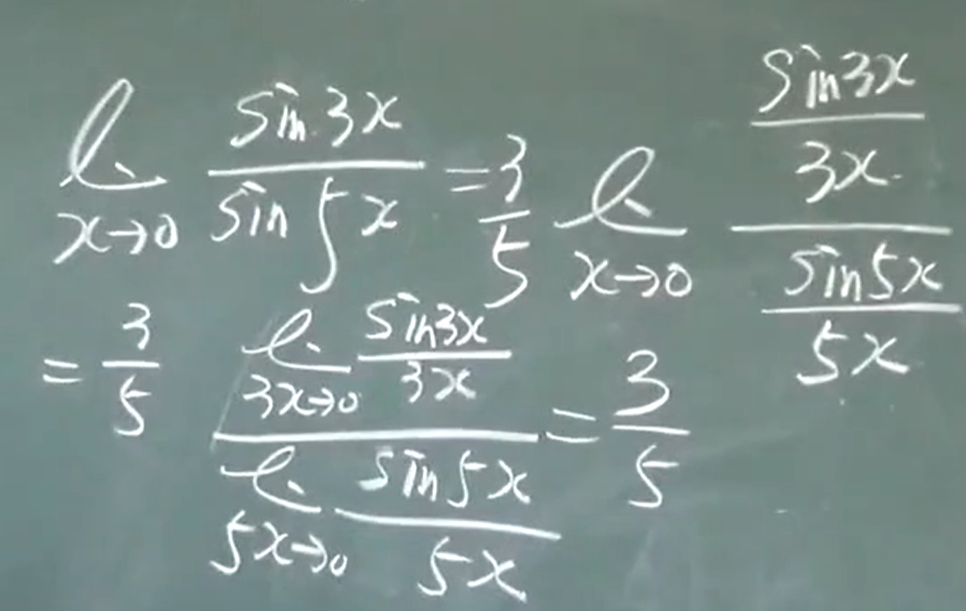
利用反函数：

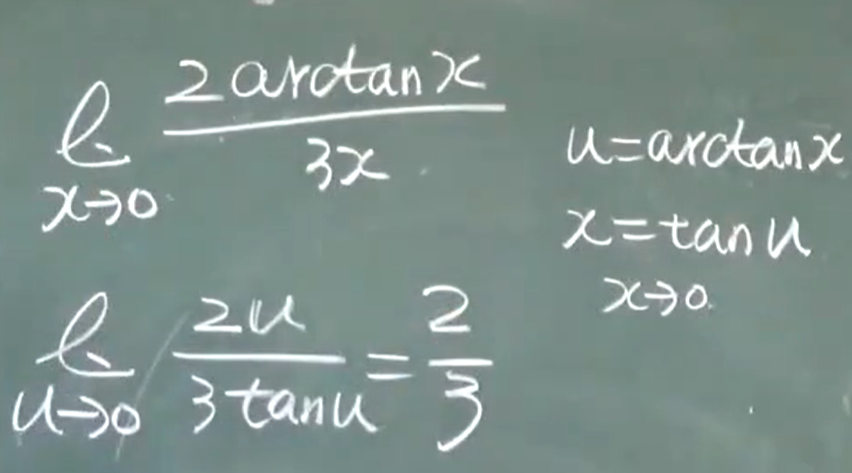
题型：

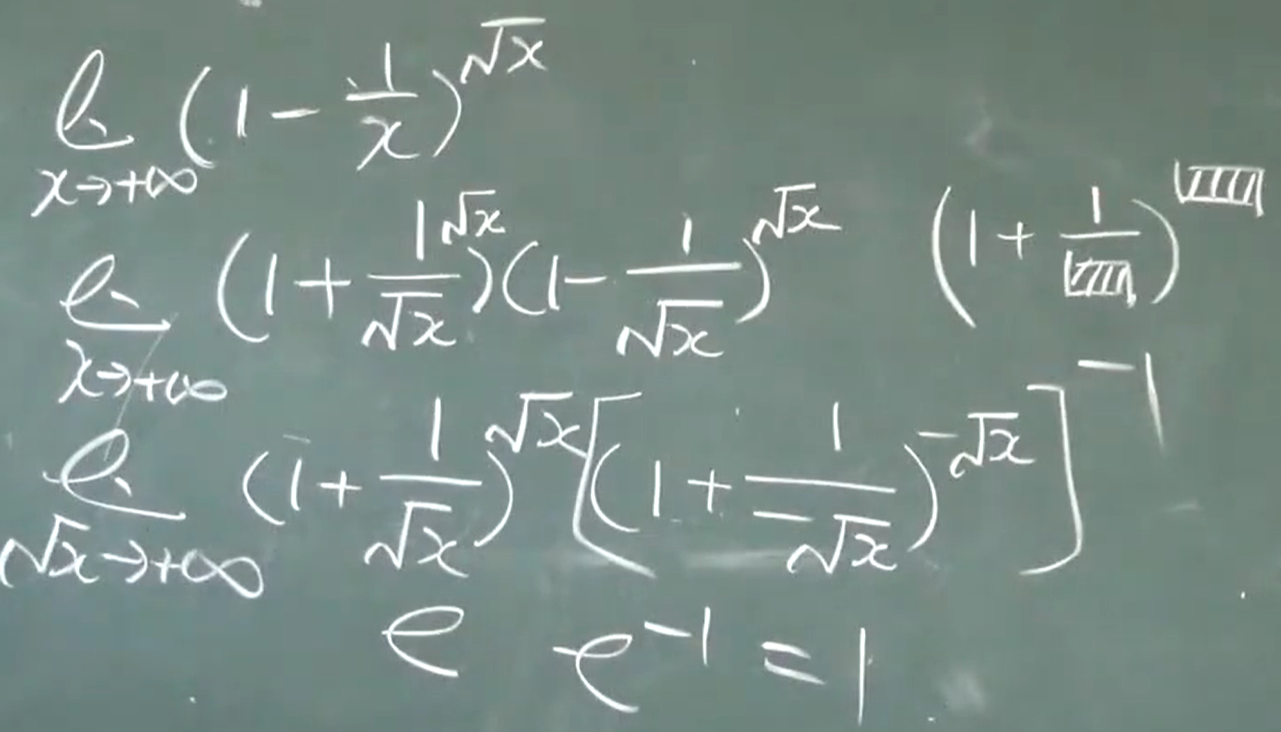
无穷小的比较

$\lim f(x)=0$ ,$\lim$ $g(x)=0$ ,$g(x)≠0$

• $\lim \frac{f(x)}{g(x)}=0$ .$f(x)$比$g(x)$高阶无穷小，$f(x)=o(g(x))$

• $\lim \frac{f(x)}{g(x)}=\infty$ .$f(x)$比$g(x)$低阶无穷小，没有符号

如: $x\to 0$ , $\frac{x}{x^2}$ ,分母的趋0速度更快， $\frac{1}{x}$

• $\lim \frac{f(x)}{g(x)}=c≠0$，同阶无穷小；

如：$x>0$ , $\frac{4x}{2x}=2$

• $\lim \frac{f(x)}{g(x)}=c=1$ , 等价无穷小$f(x)$~$g(x)$

例题：

1)$ln(1+x)$~$x$ $x\to0$

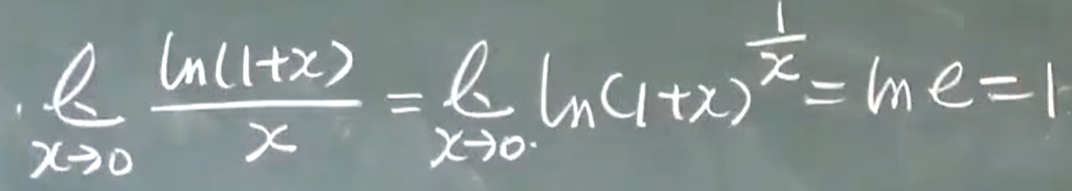
2)$e^x-1$~$x$

有个结论：

$a^x-1$~$xlna$

3)$\sqrt[n]{1+x}-1$~$\frac{1}{n}x$

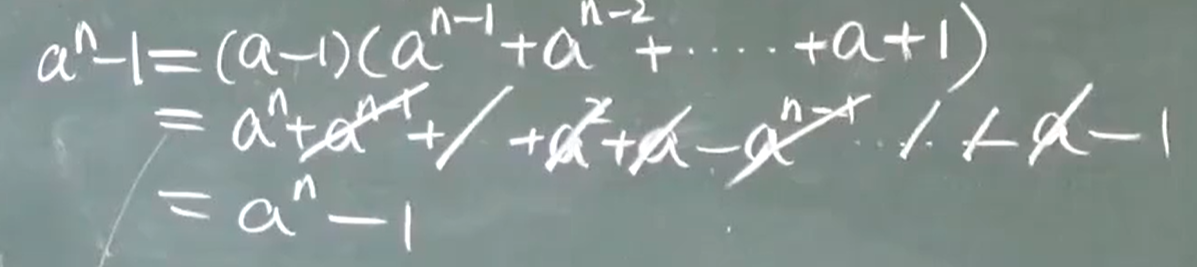
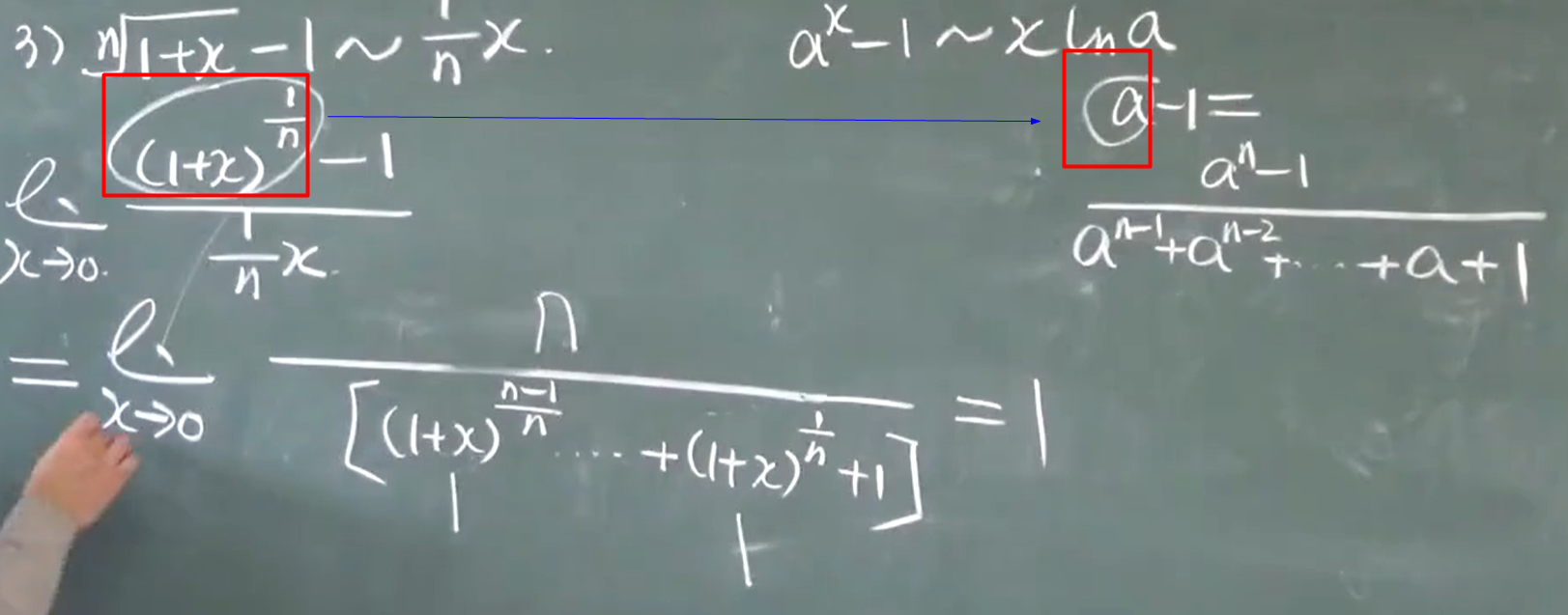
可以直接用的公式：

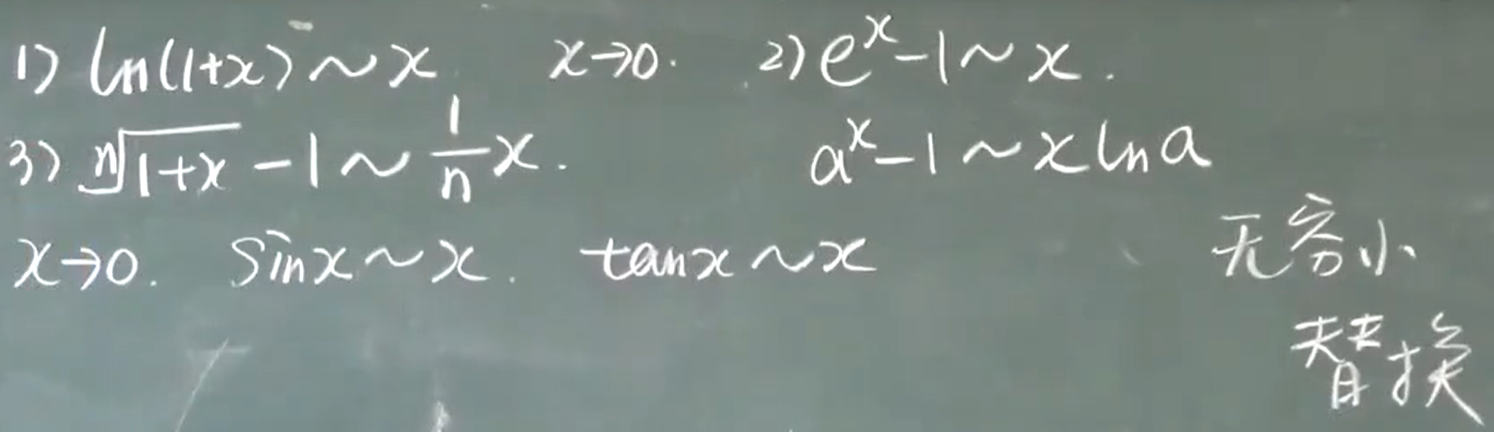
$f_1(x)$~$f_2(x)$,$g_1(x)$~$g_2(x)$ , $\lim \frac{f_2(x)}{g_2(x)}$存在极限

$\lim \frac{f_1(x)}{g_1(x)}$ = $\lim \frac{f_2(x)}{g_2(x)}$

1）两个无穷小之比才用

2）分子或分母是因子的乘积，选部分因替换

$\frac{(●)×(●)×(■)}{(●)×(■)}$

只保留■。

例题：

∵ $sinx$~$x$