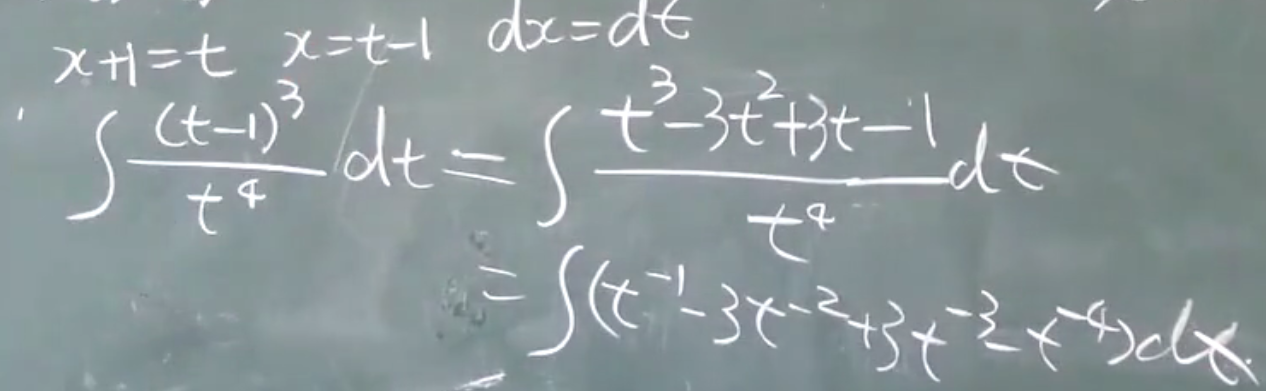$F’(x)=f(x)$

$F(x)$是$f(x)$的一个原函数.

F(x)是f(x)的一个原函数，F(x)+c也是f(x)的原函数

$f(x)$是$F’(x)$的导函数.

知道$F’(x)$,$f(x)$只有唯一一个

知道$f(x)$,$F’(x)$可以有无穷多个

不定积分

$f(x)$的原函数的全体

$\int_{}{}f(x) \text{d}x$

$\int_{}{}$: sum,积分符号

$x$: 积分变量

$f(x)$: 被积函数

$\int_{}{}f(x) \text{d}x = F(x)+c$

例题

1. $\int_{}{}x^2 \text{d}x = \frac{1}{3}x^3+c$

几何意义

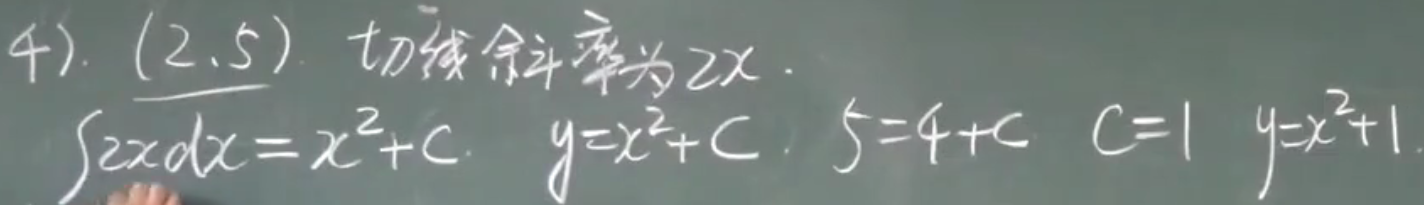
性质

$$\int_{}{}kf(x)\text{d}x=k\int_{}{}f(x)\text{d}x$$

k可以朝外拿：

①k是常数

②k是与x无关的另变量

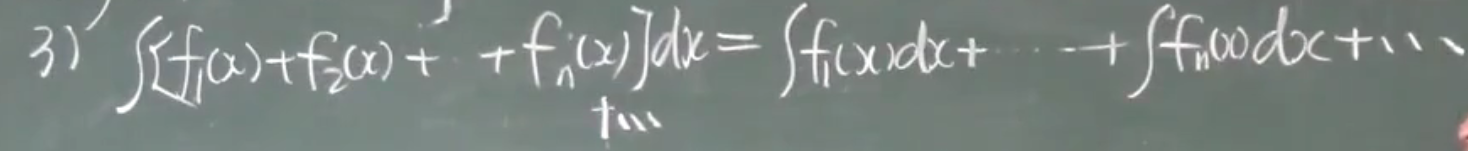
有限个可以，但无限个不能

基本积分公式

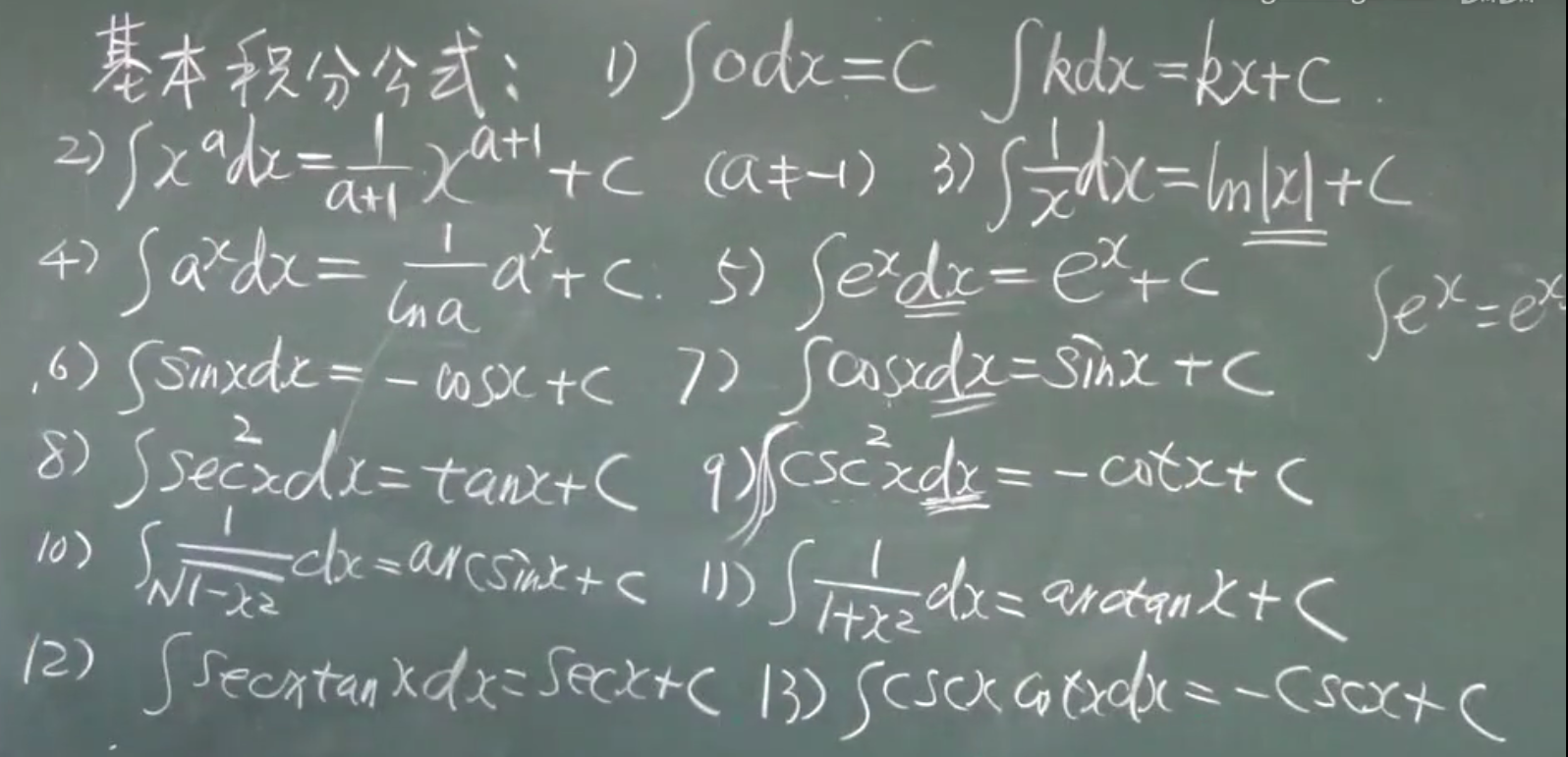
例题：

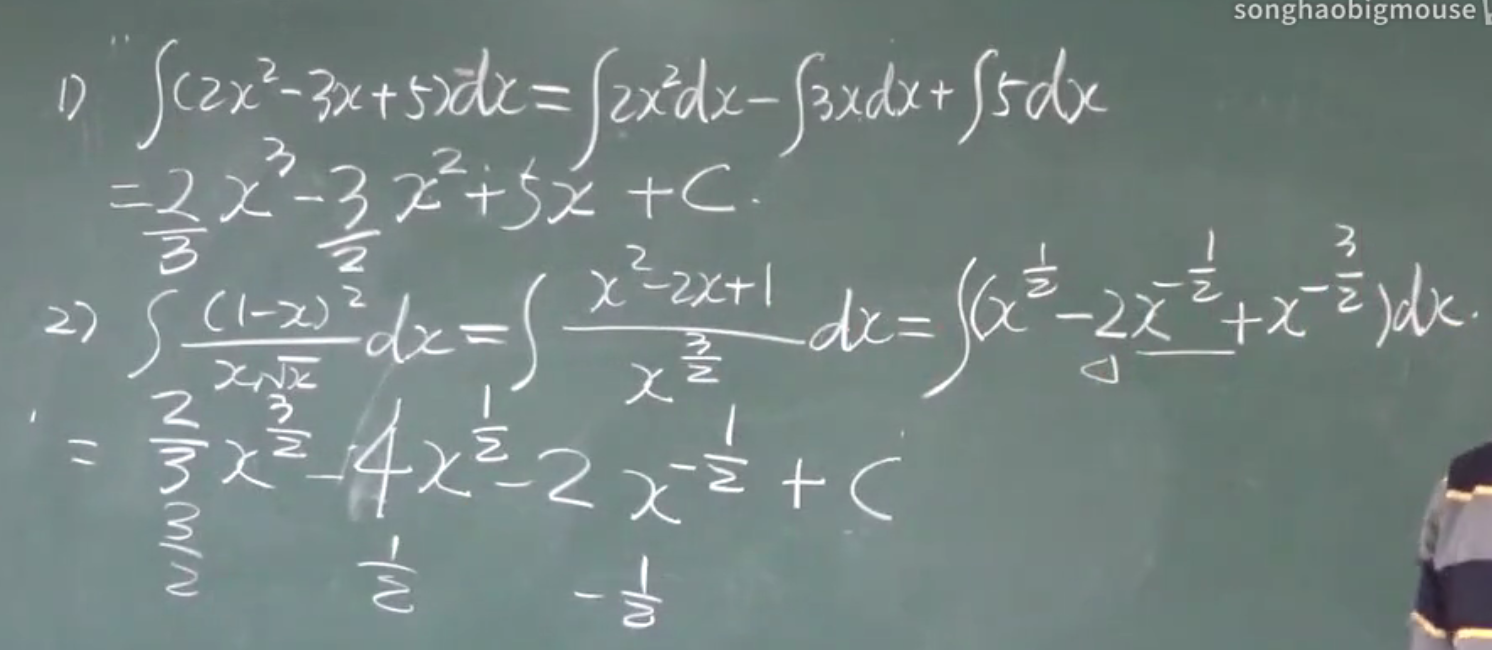
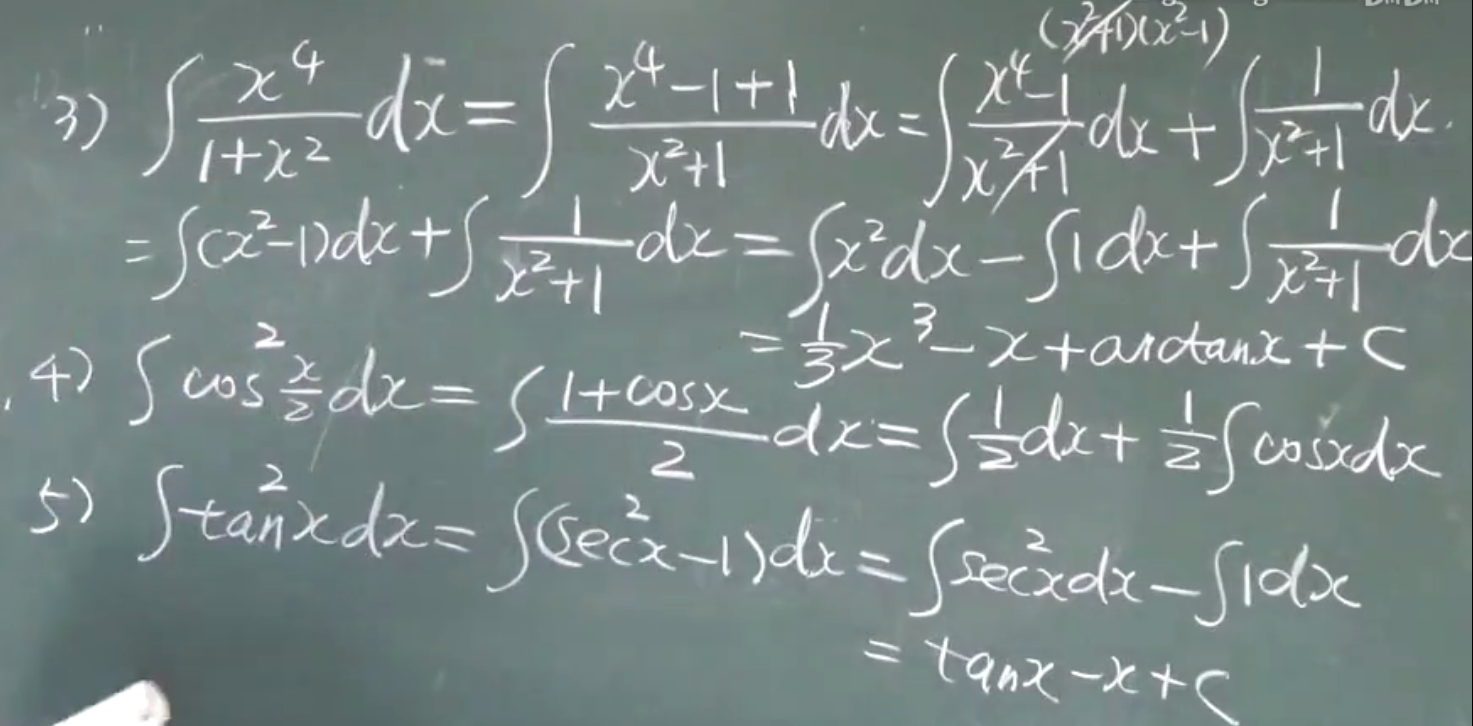
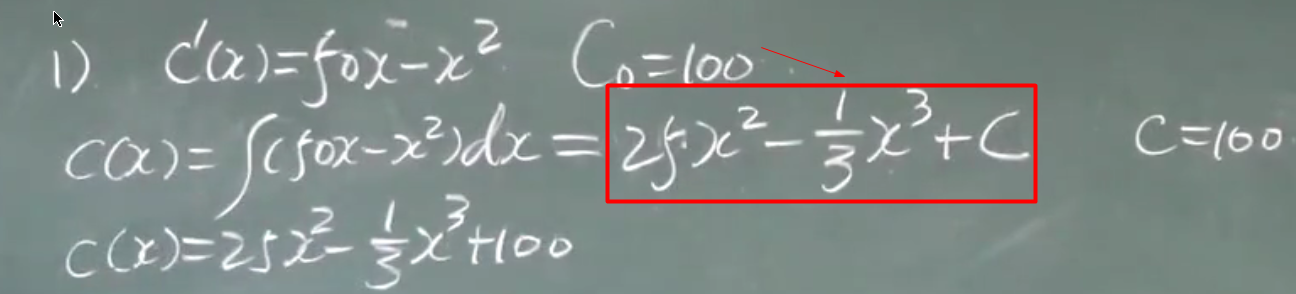
积分法

第一换元积分法(凑微分法)

求原函数

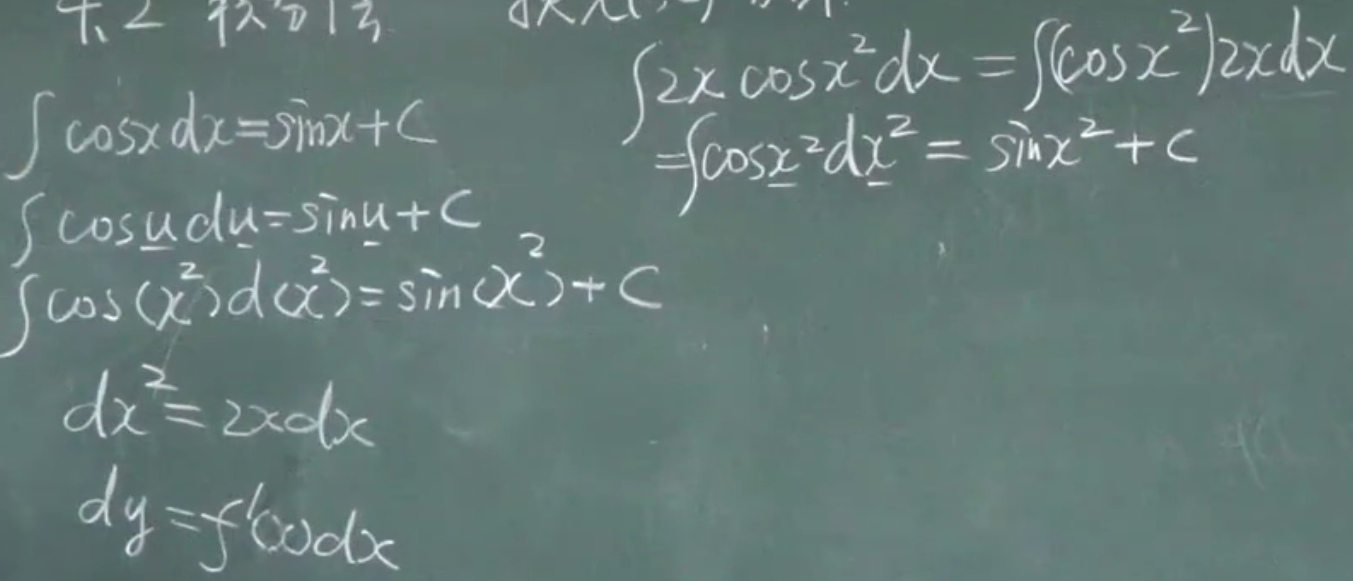
1）把d外面的某项拿到d里面(变成原函数)

2）凑基本积分公式

例题：

dk()=kd()

d()里面的项可以随意加减常数

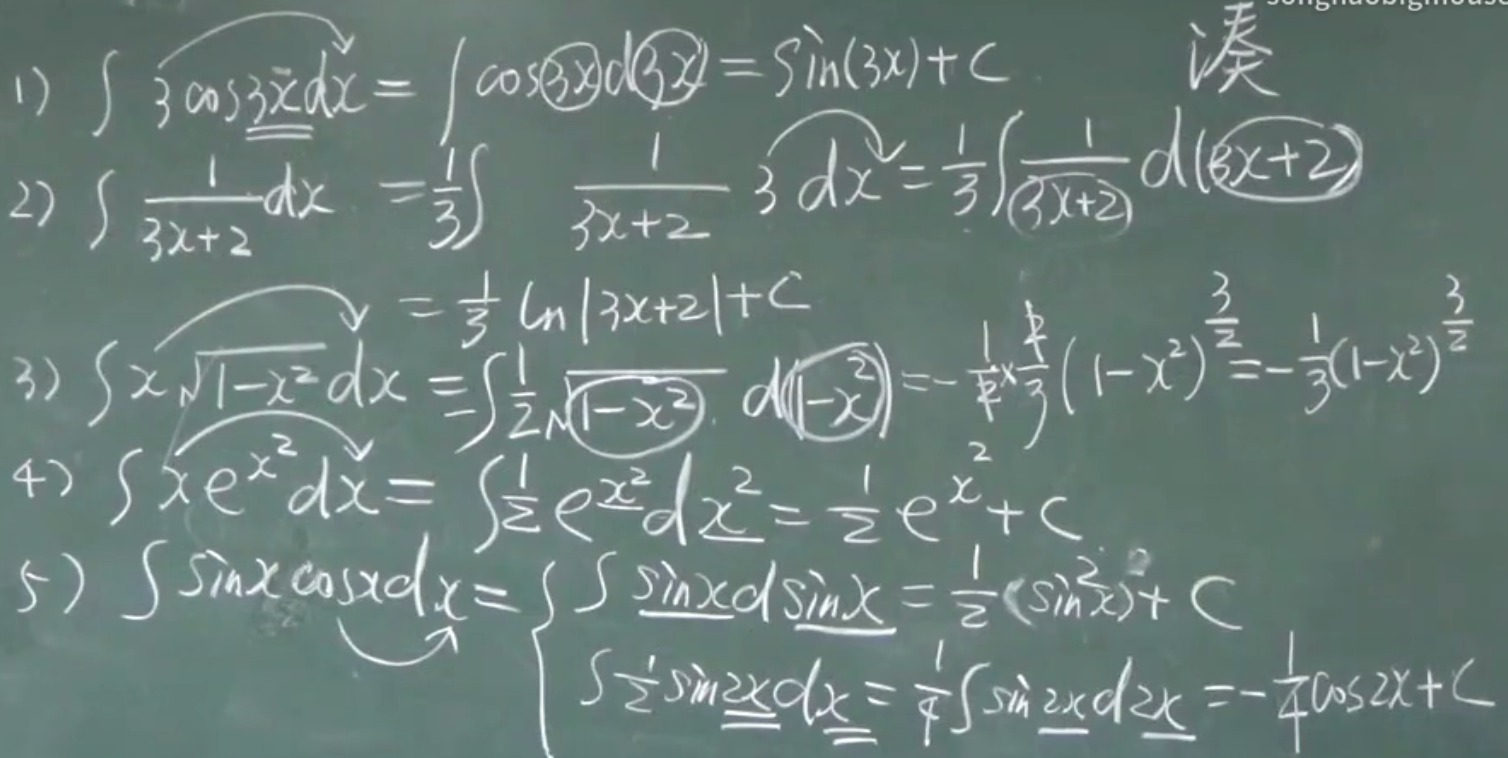
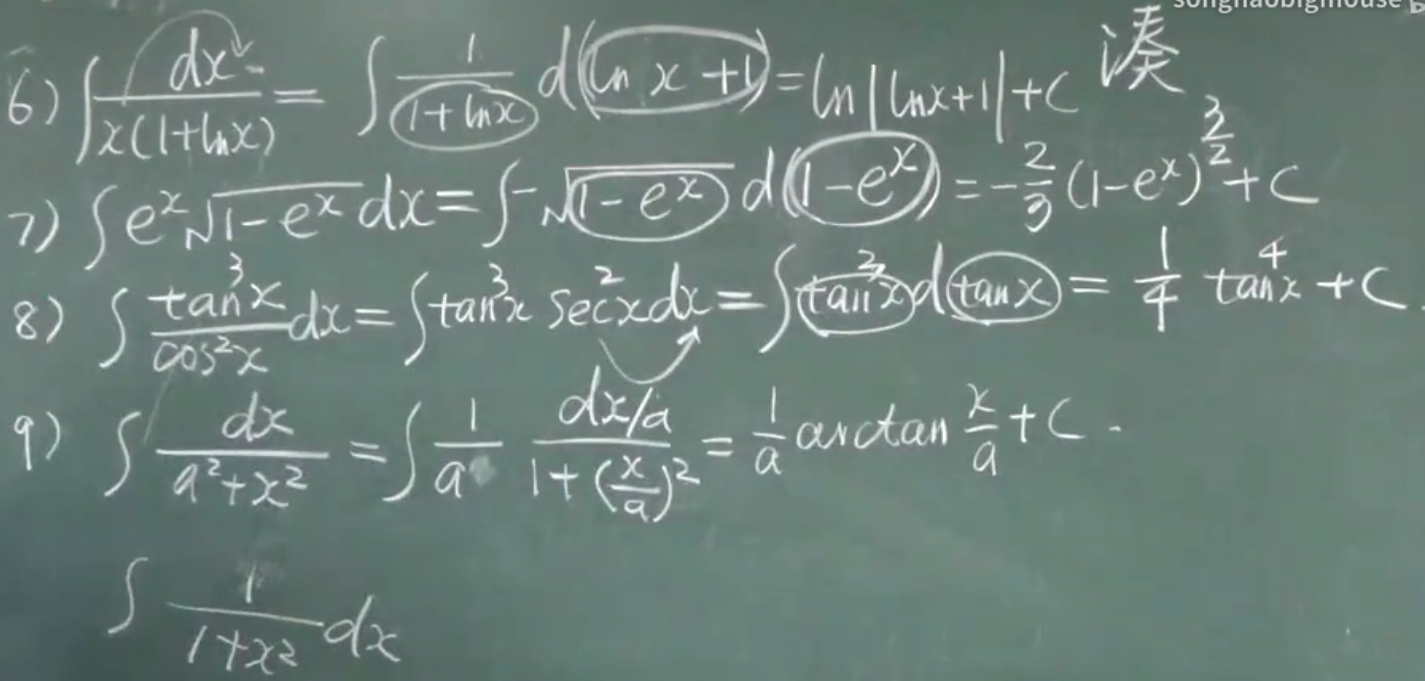
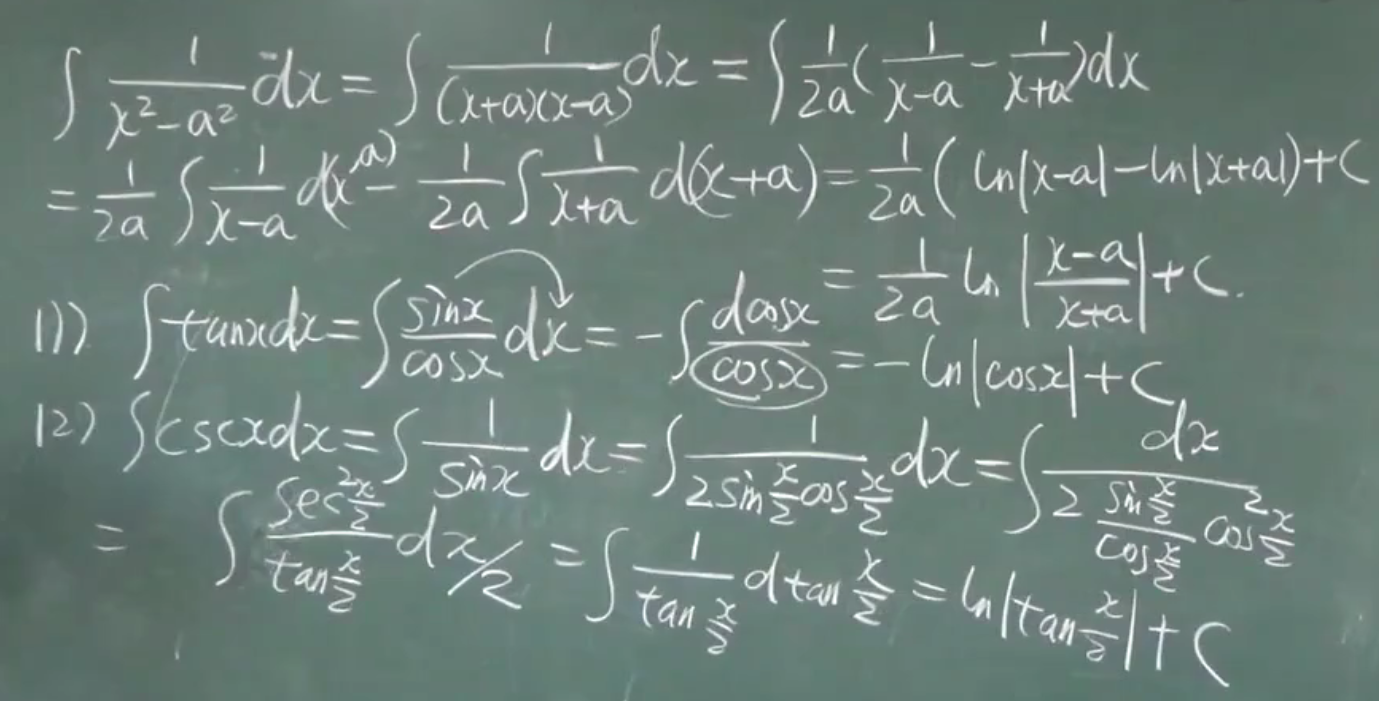
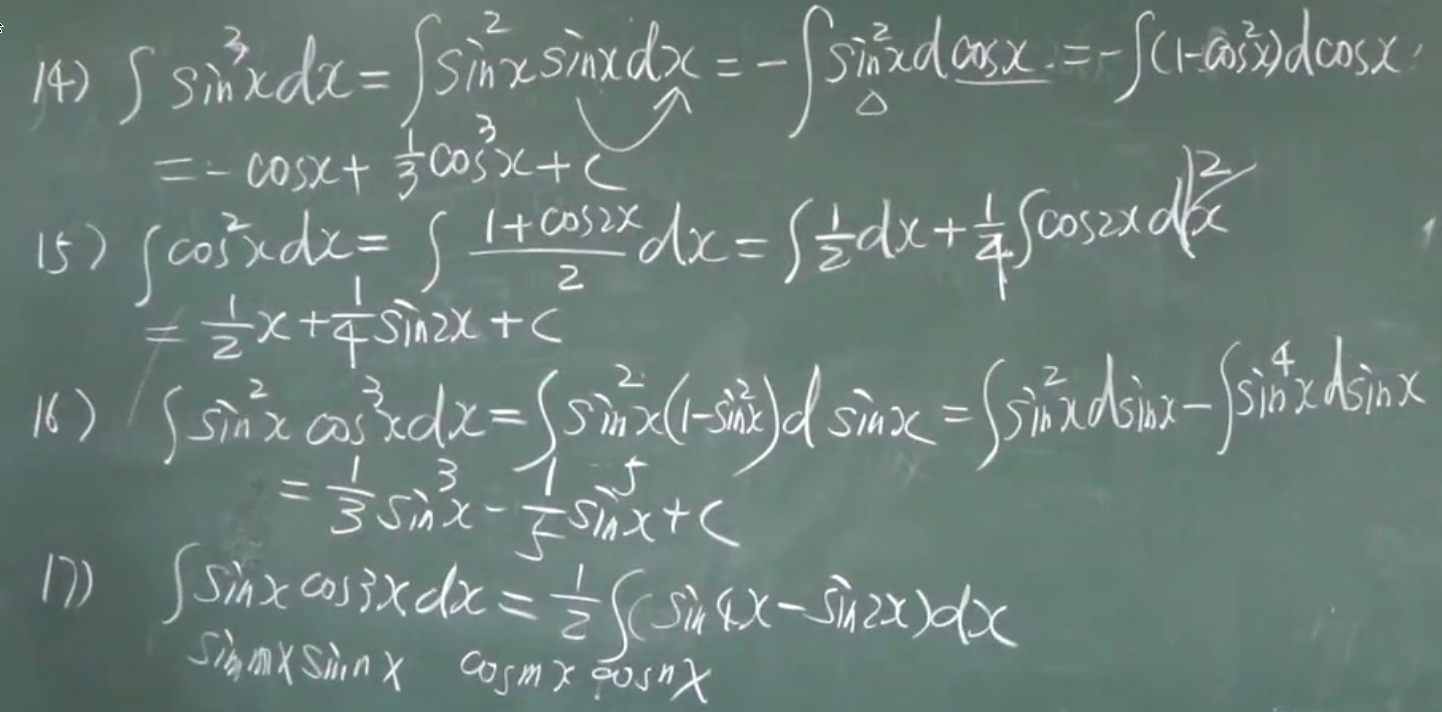
第二换元积分

求导

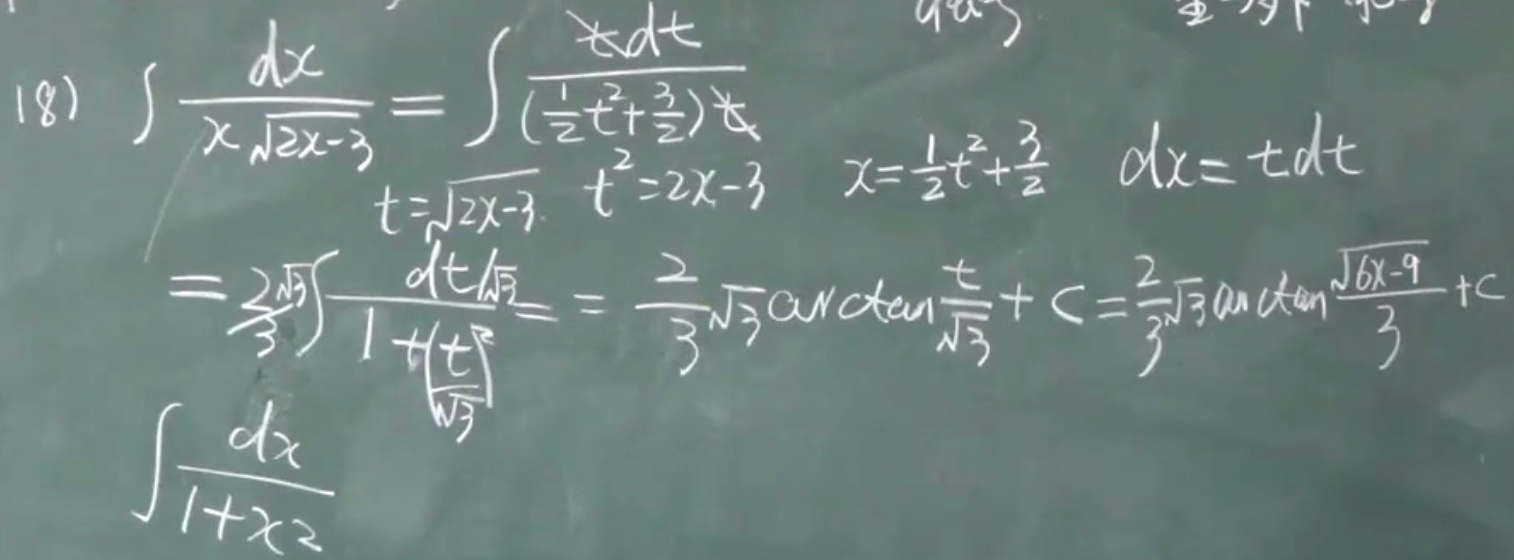
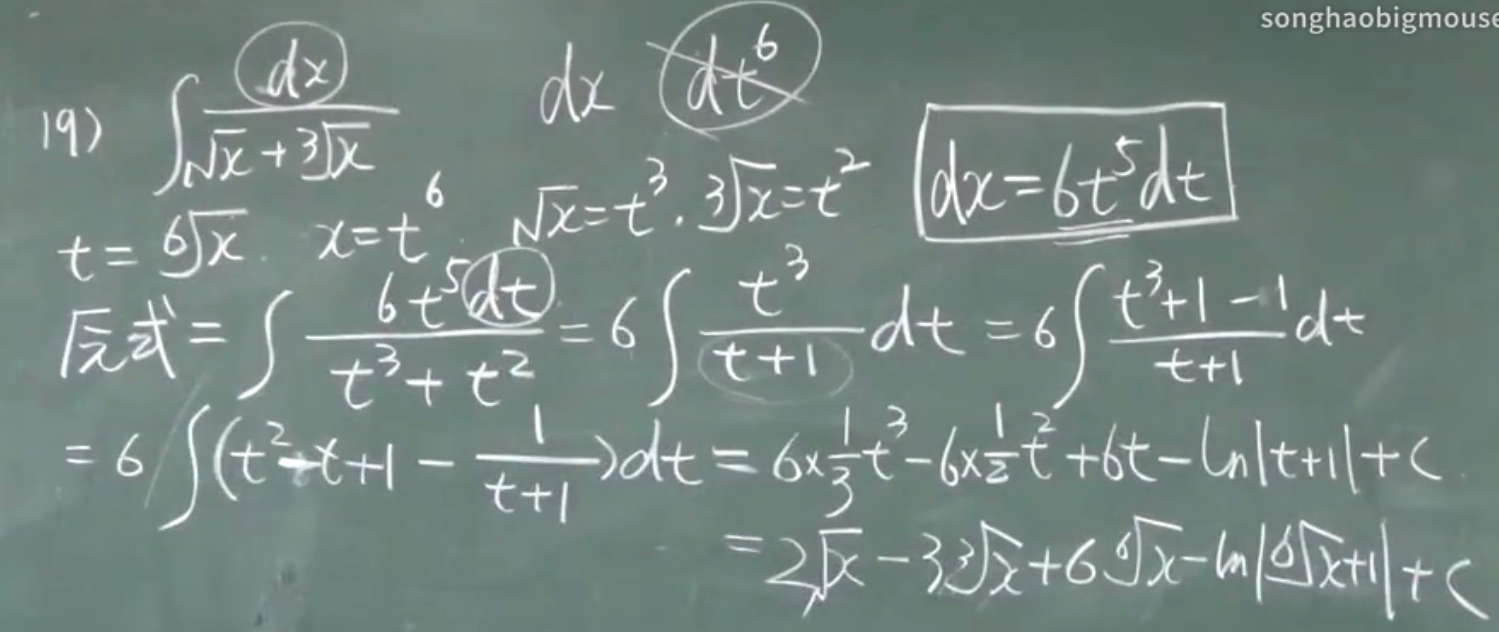
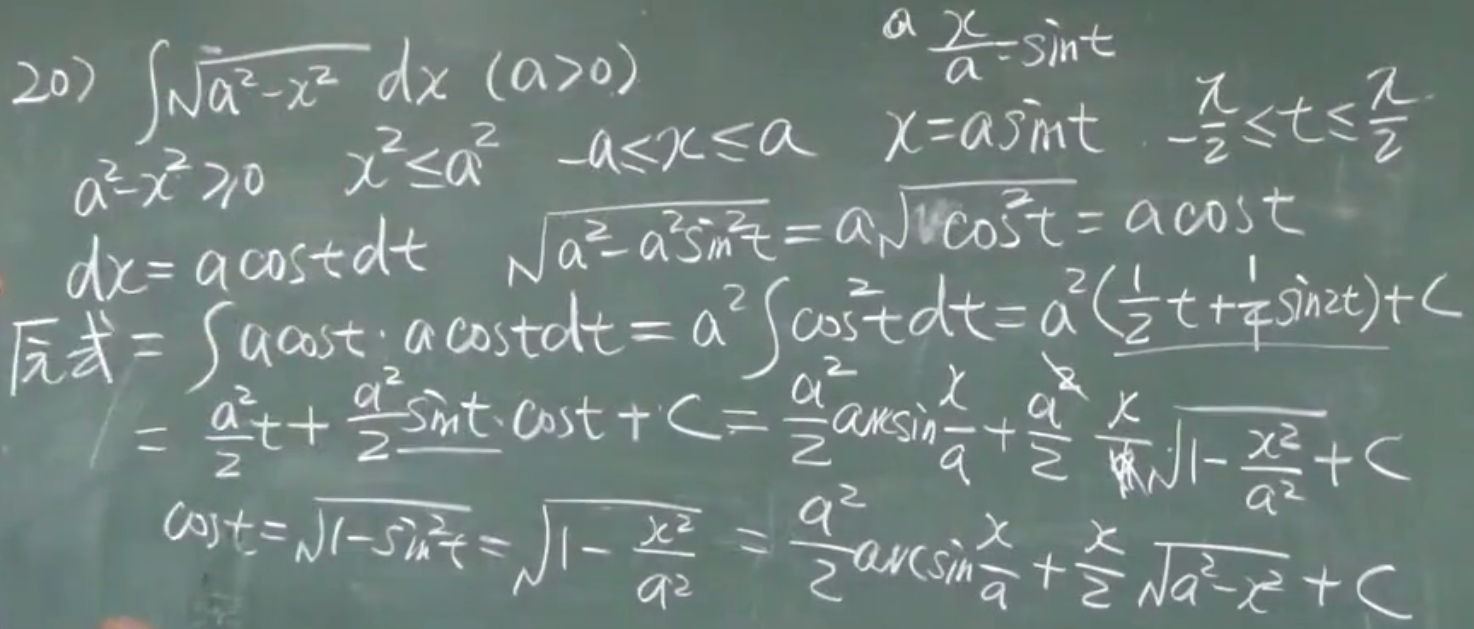
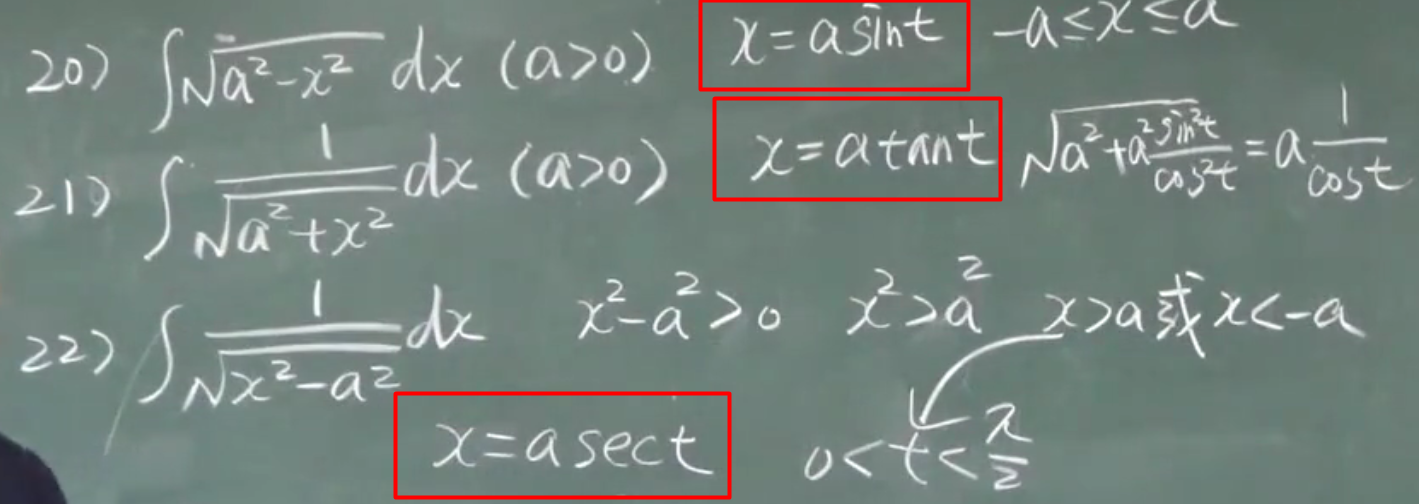
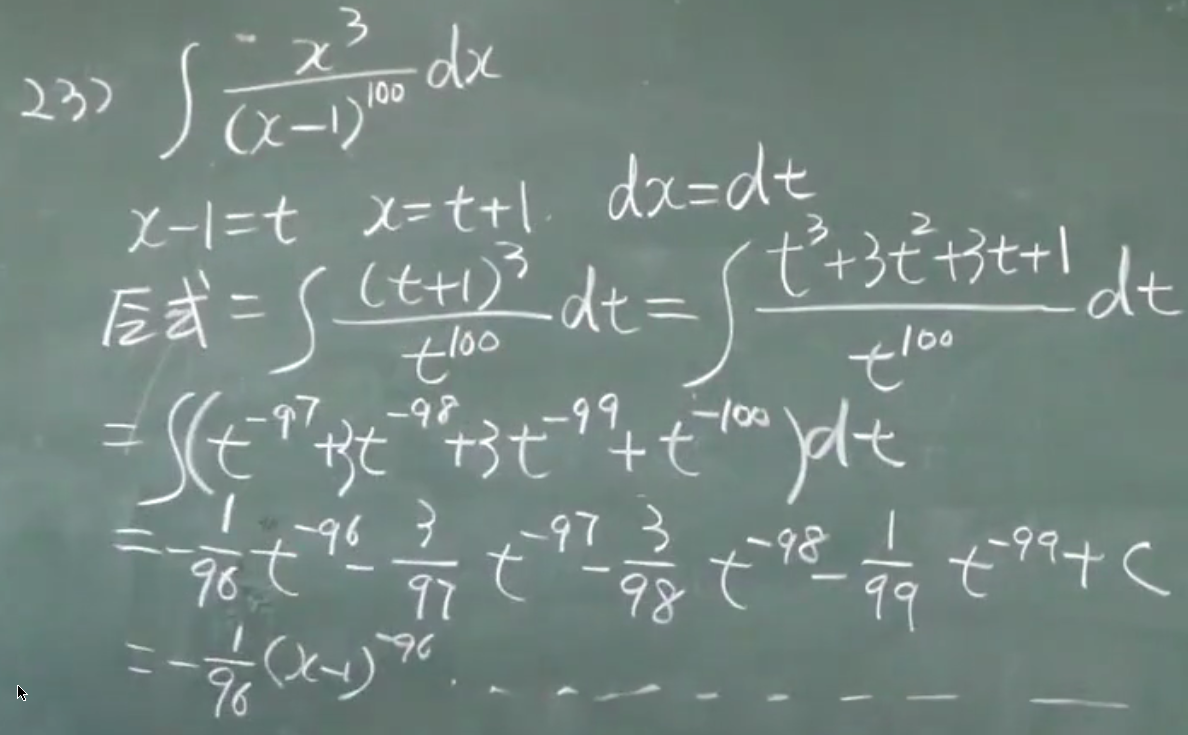
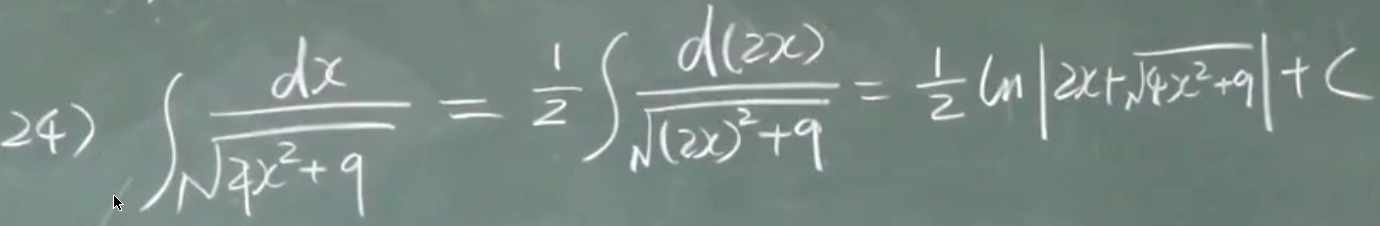
公式

分部积分法

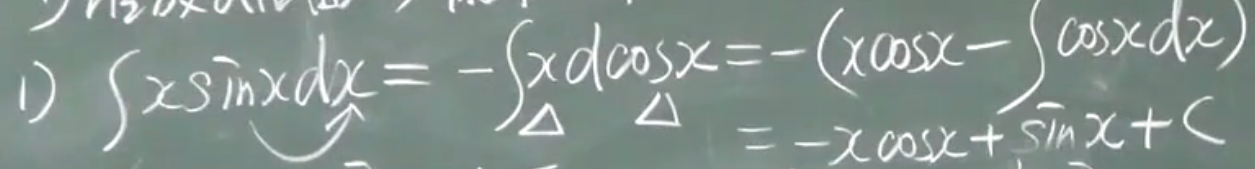
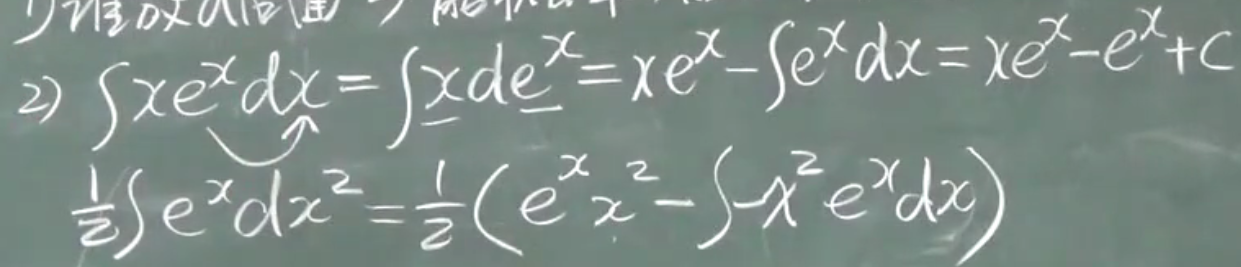
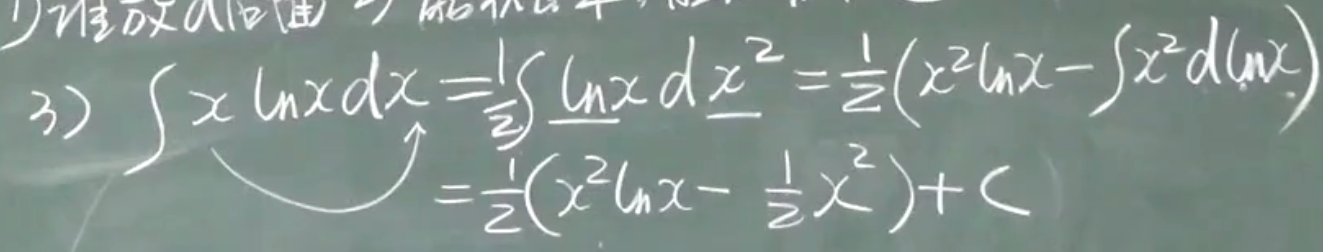
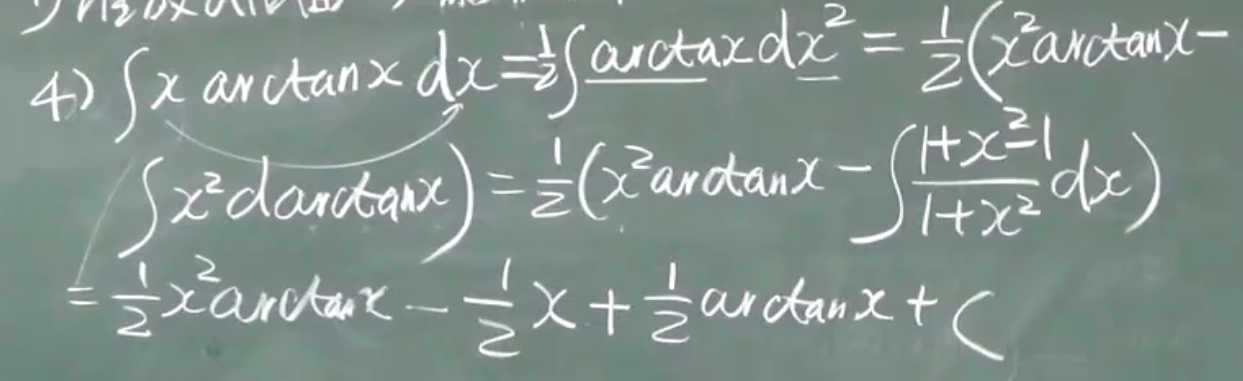
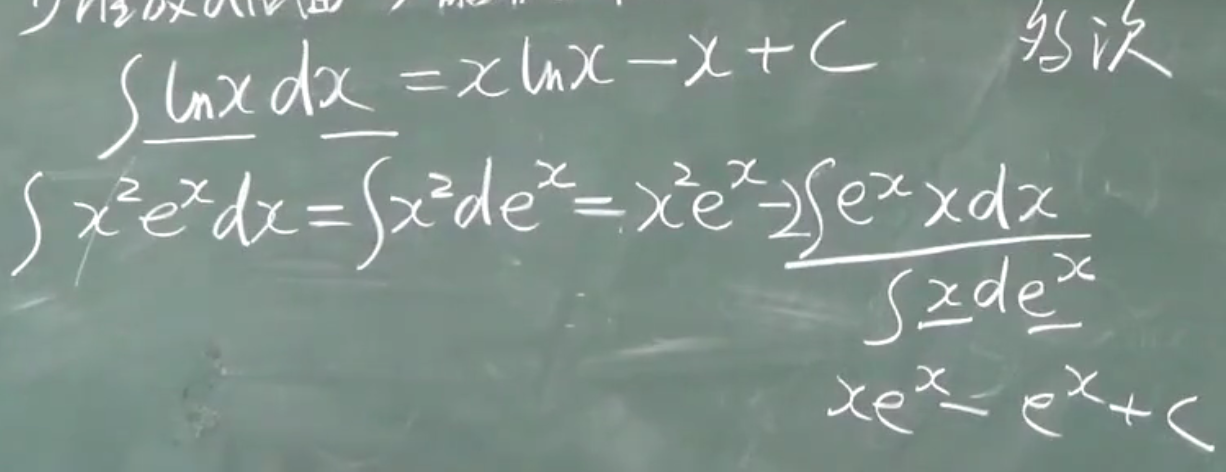
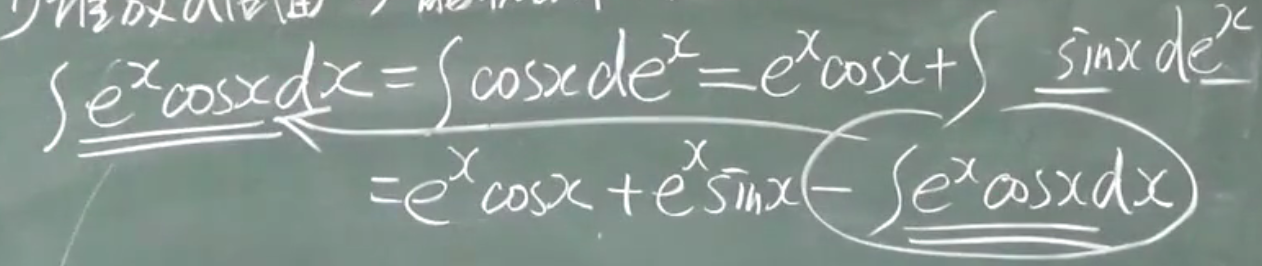
优先：

$e^x,sinx,cosx,x(x^n),lnx,arctanx$

有理函数积分

分子的最高次数比较高：

最高次数相等(最终使分母次数高)：

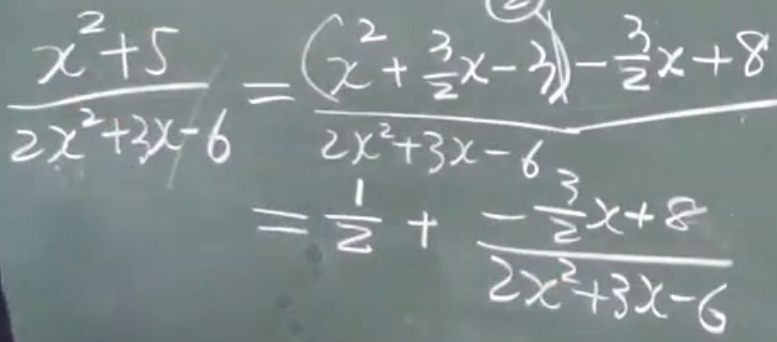
所有方法都要化成分母次数比分子次数高。

真分式

分母次数比分子次数高的叫做真分式

第一类题目

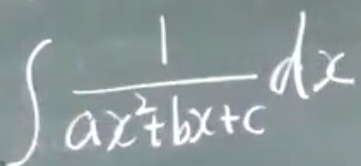
1）$b^2-4ac=0$ $ax^2+bx+c=0$

$a(x-x_1)^2=0$

例如：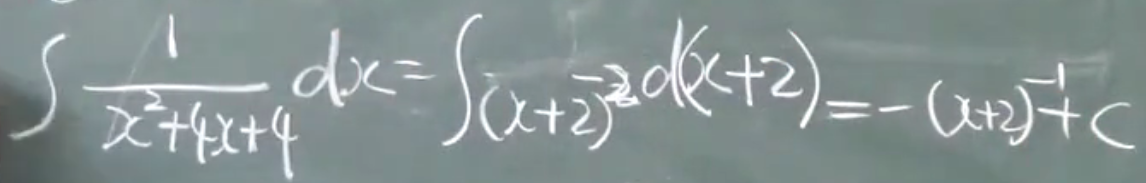

2）$b^2-4ac>0$ $ax^2+bx+c=0$有两个不等的根

$a(x-x_1)(x-x_2)=0$

待定系数法：

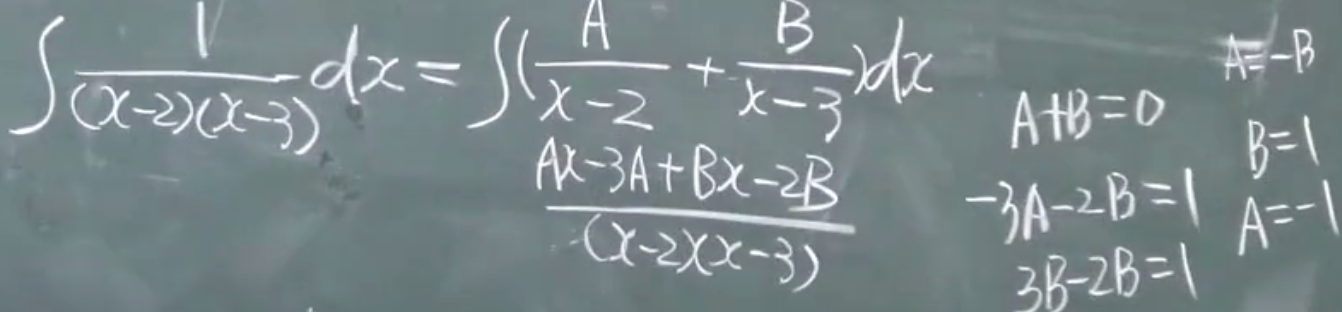
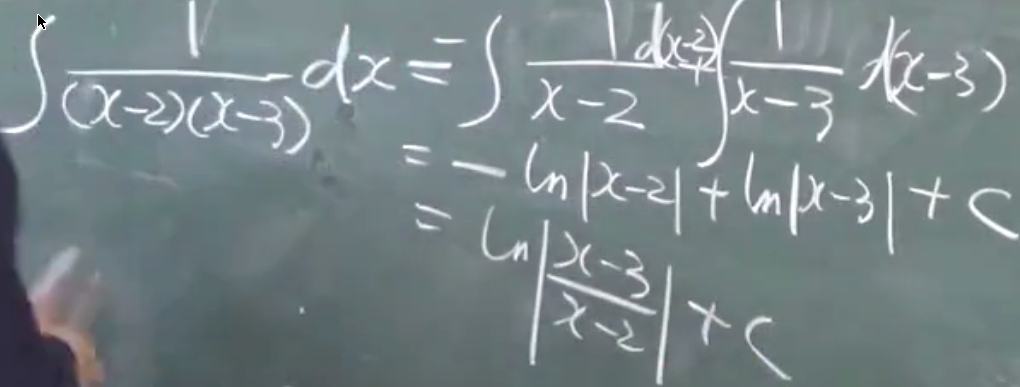
3）$b^2-4ac<0$ $ax^2+bx+c=0$没有实根

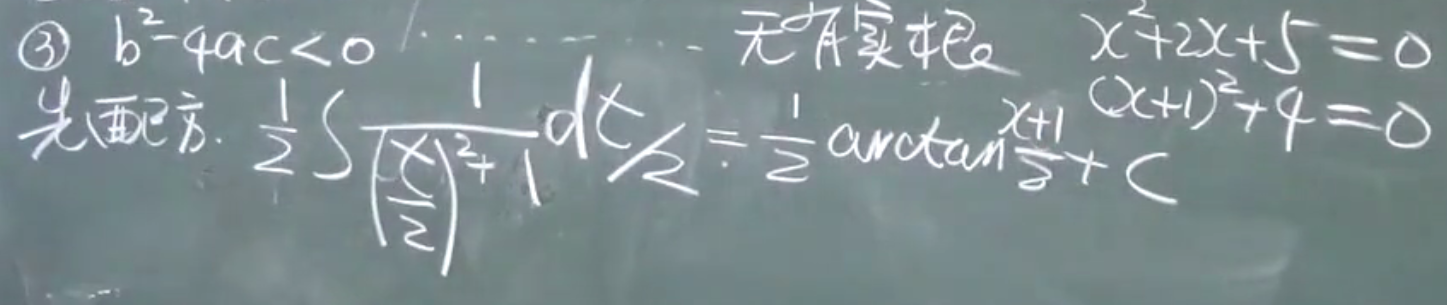
第二类题目

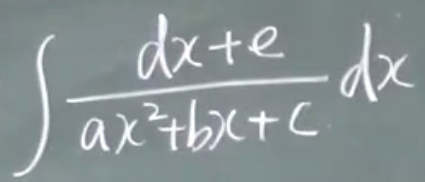
1）$b^2-4ac=0$ $ax^2+bx+c=0$

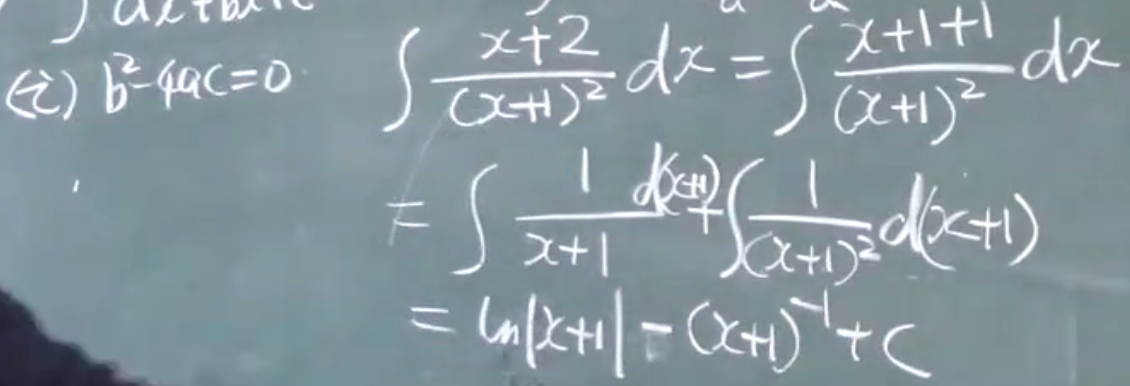
2）$b^2-4ac>0$

待定系数法：

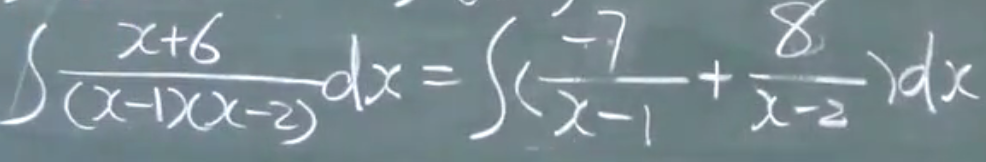
3）$b^2-4ac<0$

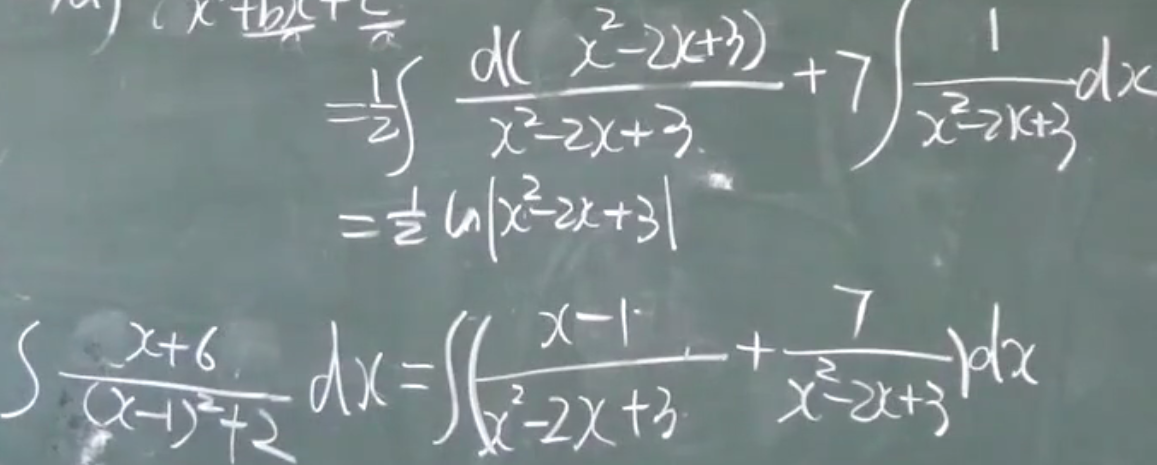
第三类题目

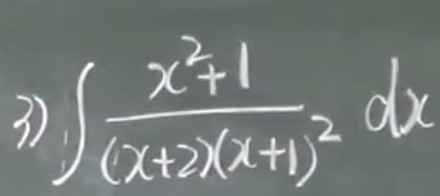
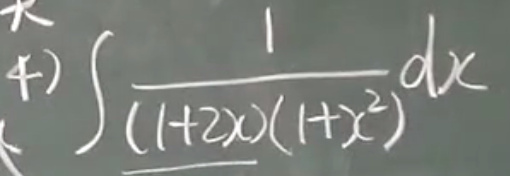
第一类表达式

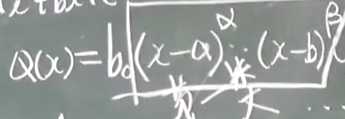
比如：

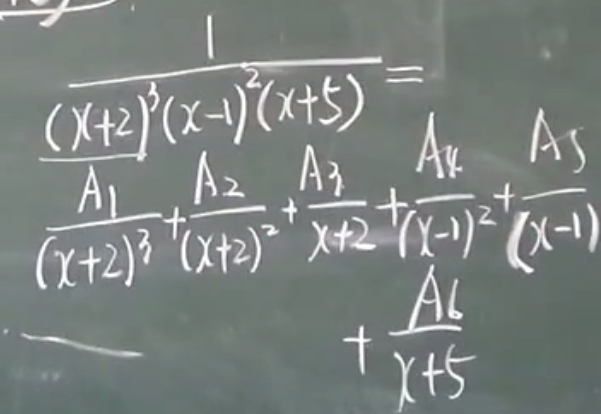
3）

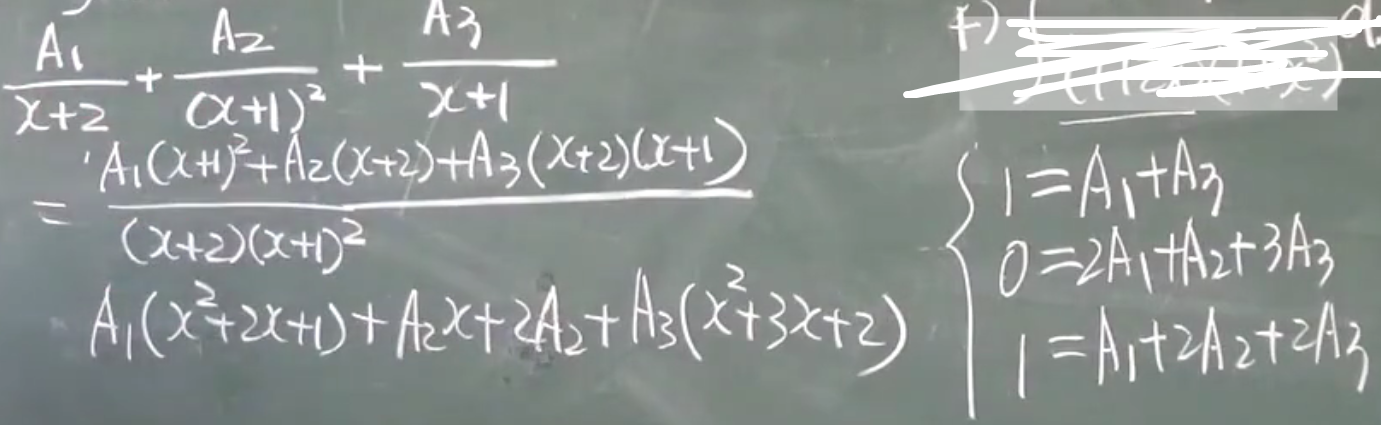
第二类

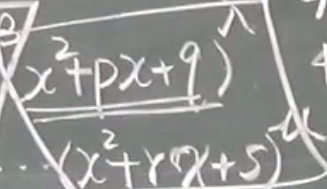
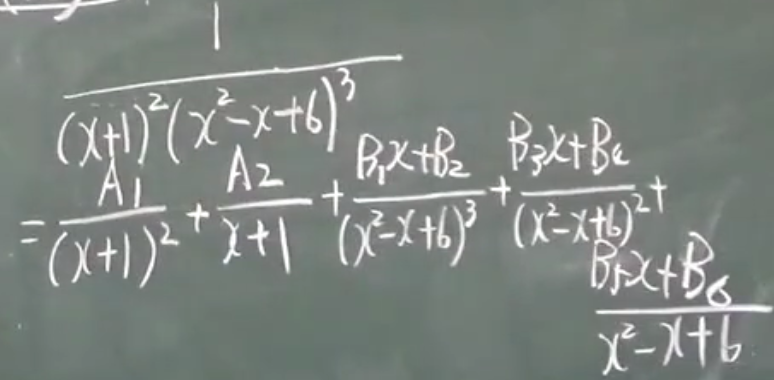
解法：

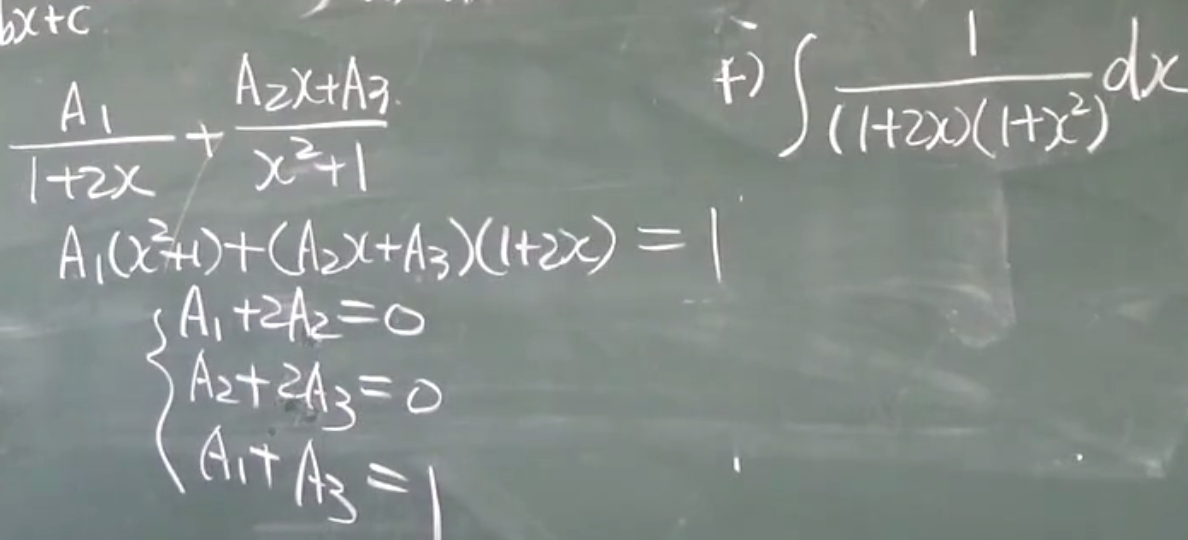
左右相等：

$A_1+2A_2=0$平方项

$A_2+2A_3=0$1次项

$A_1+A_3=1$常数项

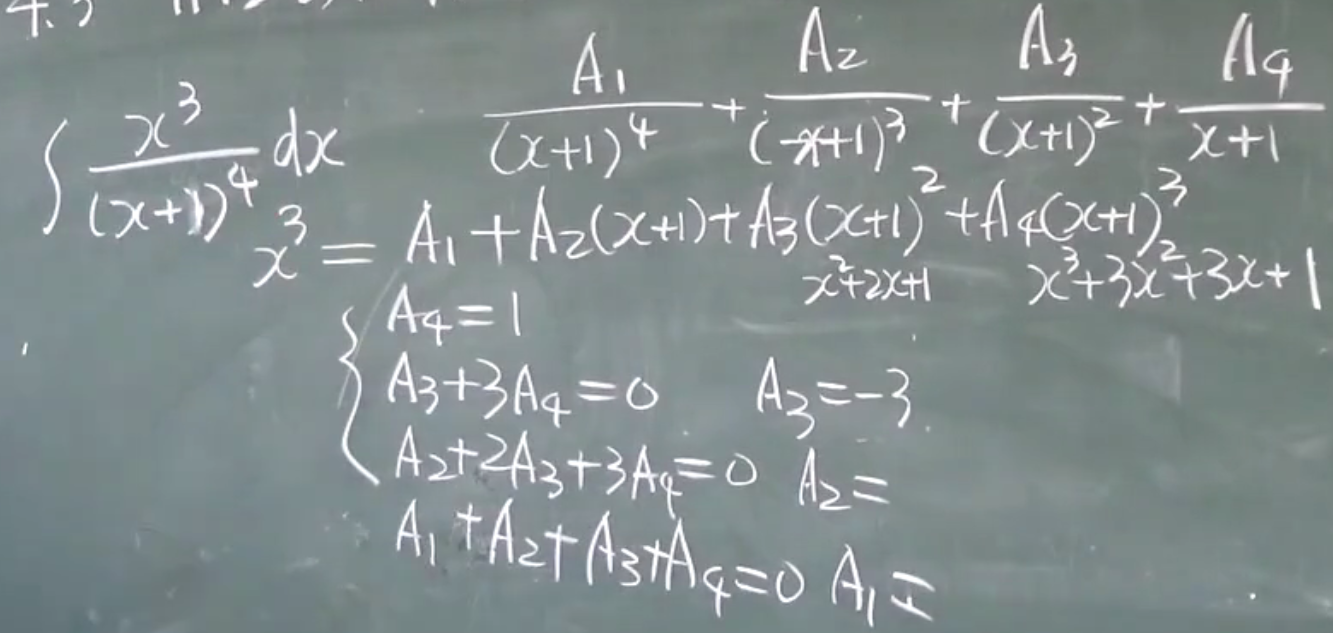
或者：