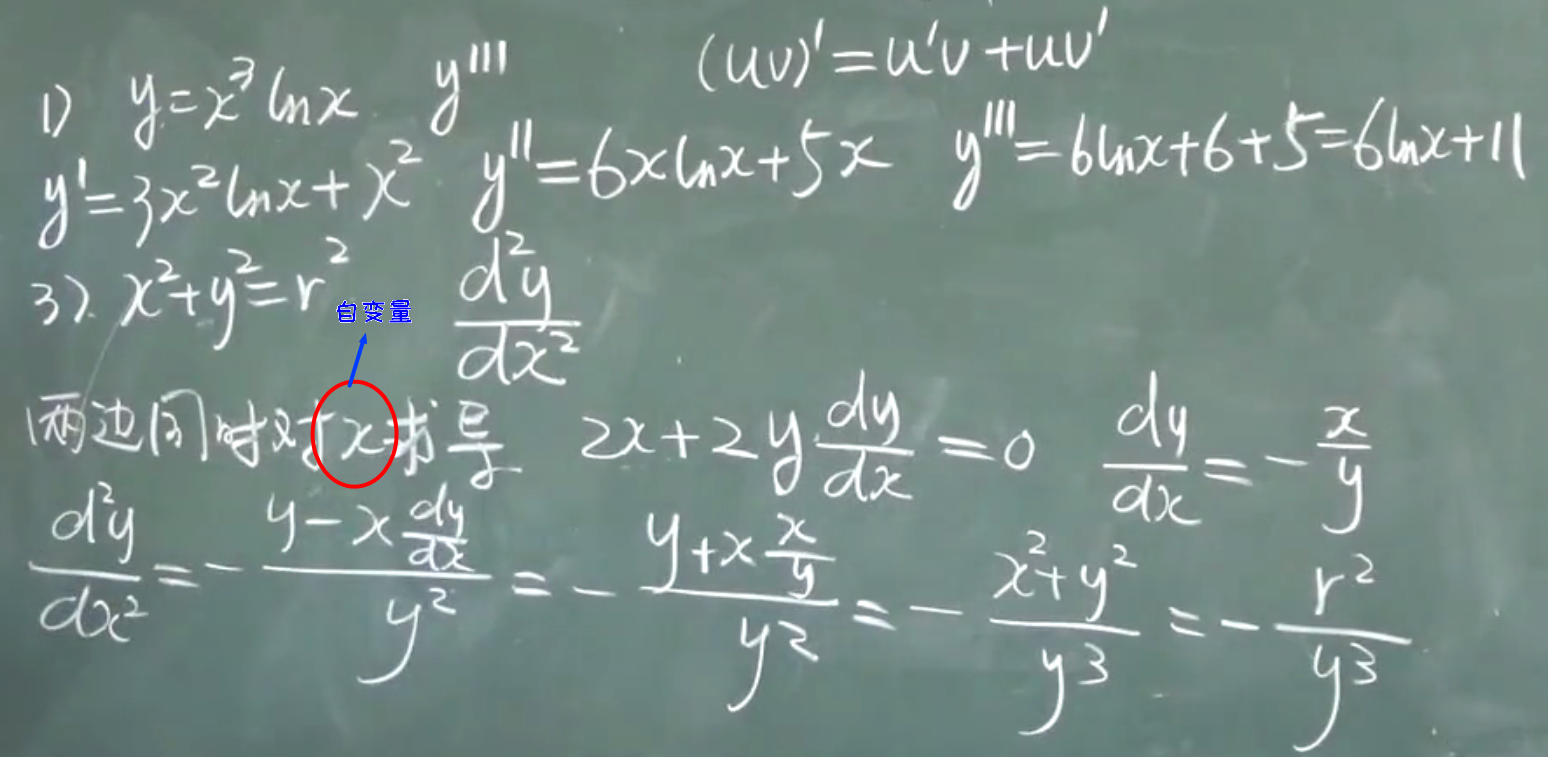变化率

$x_0 \to x_0+△x$.

$f(x_0) \to f(x_0+△x)$

$\frac{f(x_0+△x)-f(x_0)}{△x}$

从x_0到x_0+△x的平均变化率

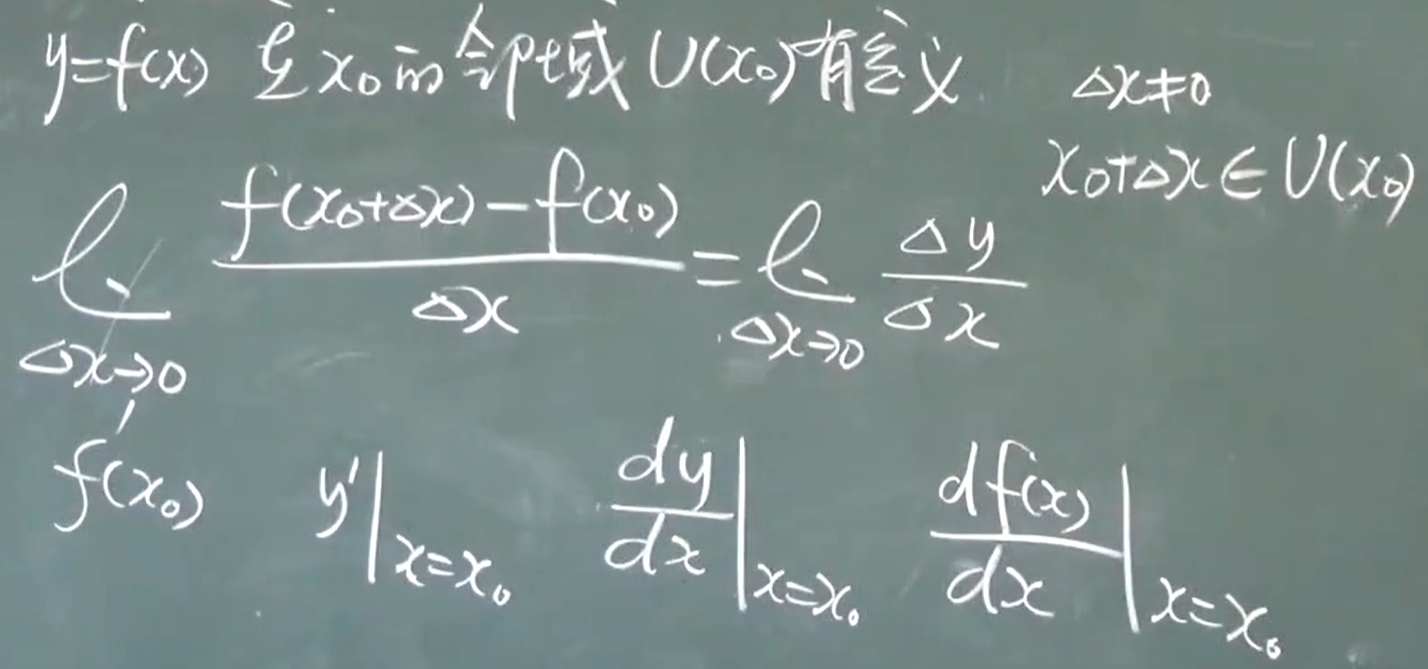
导数的四个符号

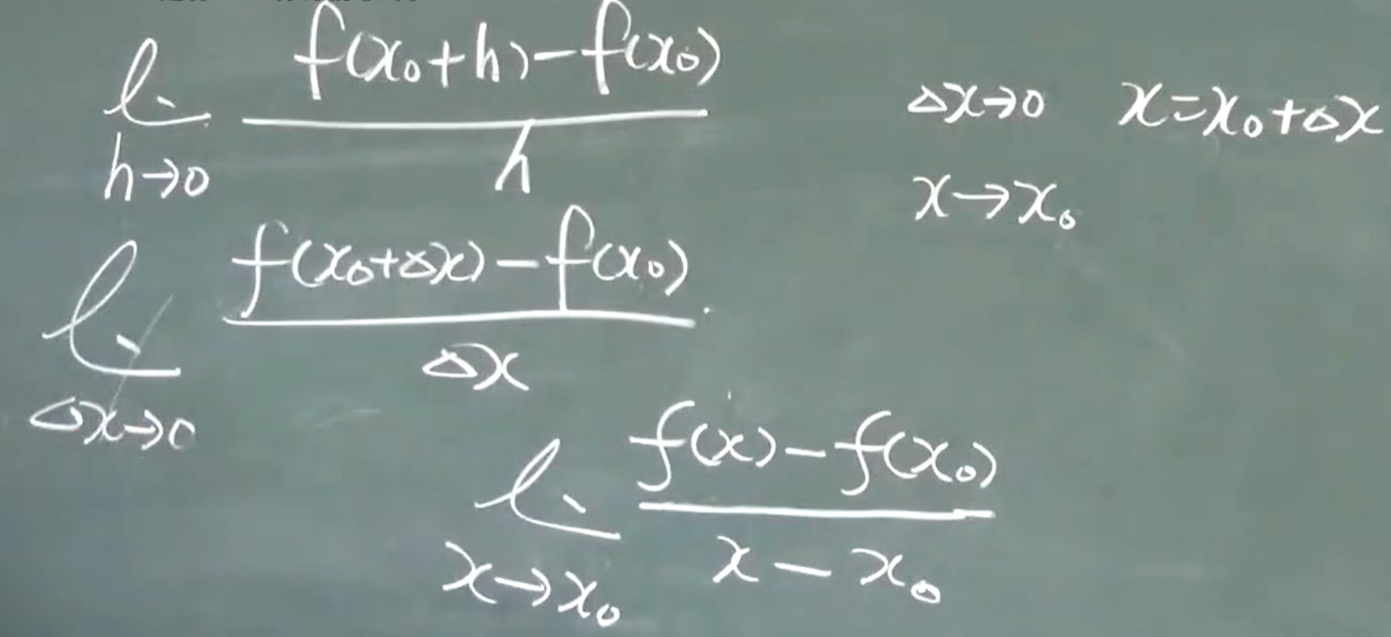
导数的三种表达方式

例题：

$y=x^2$

$y'$

$y’|_{x=2}$

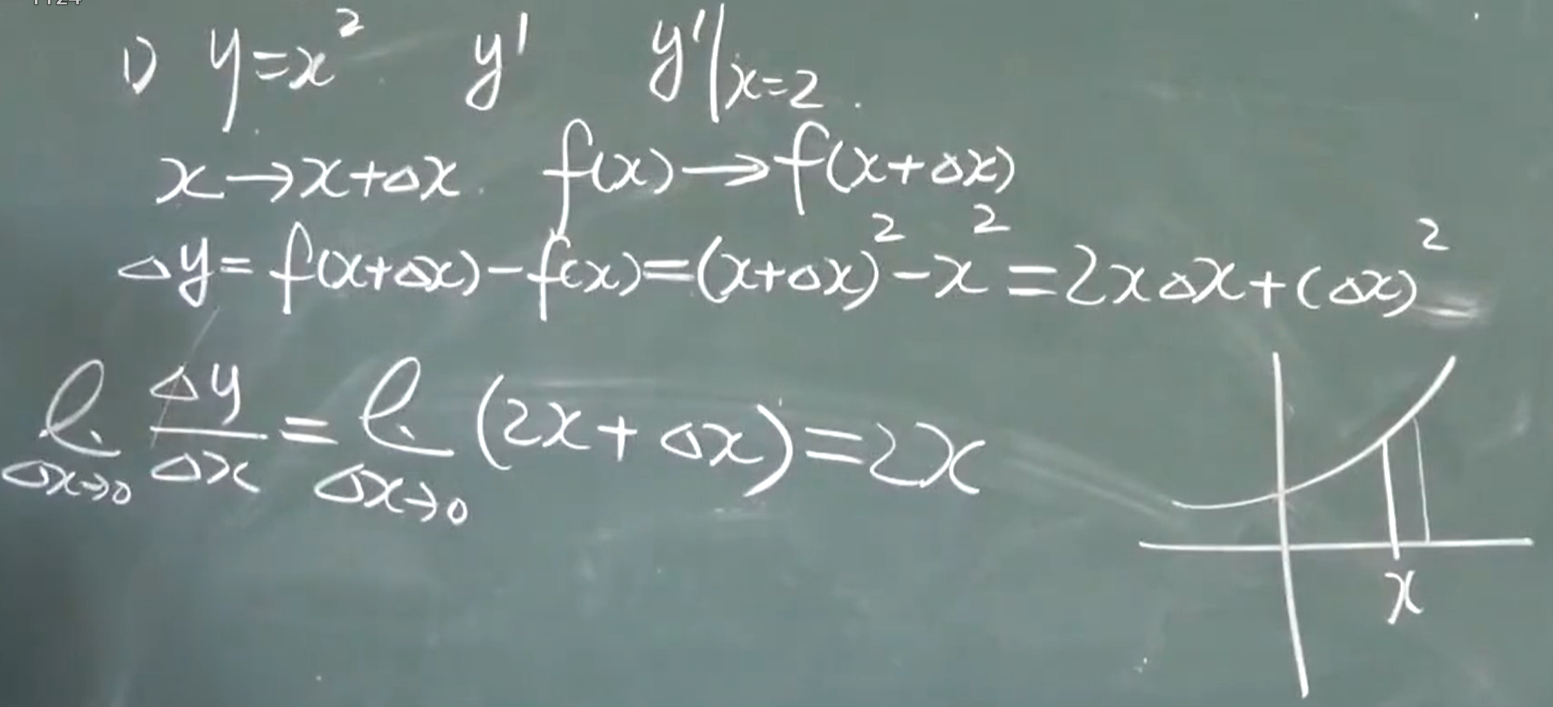
=4;

求导

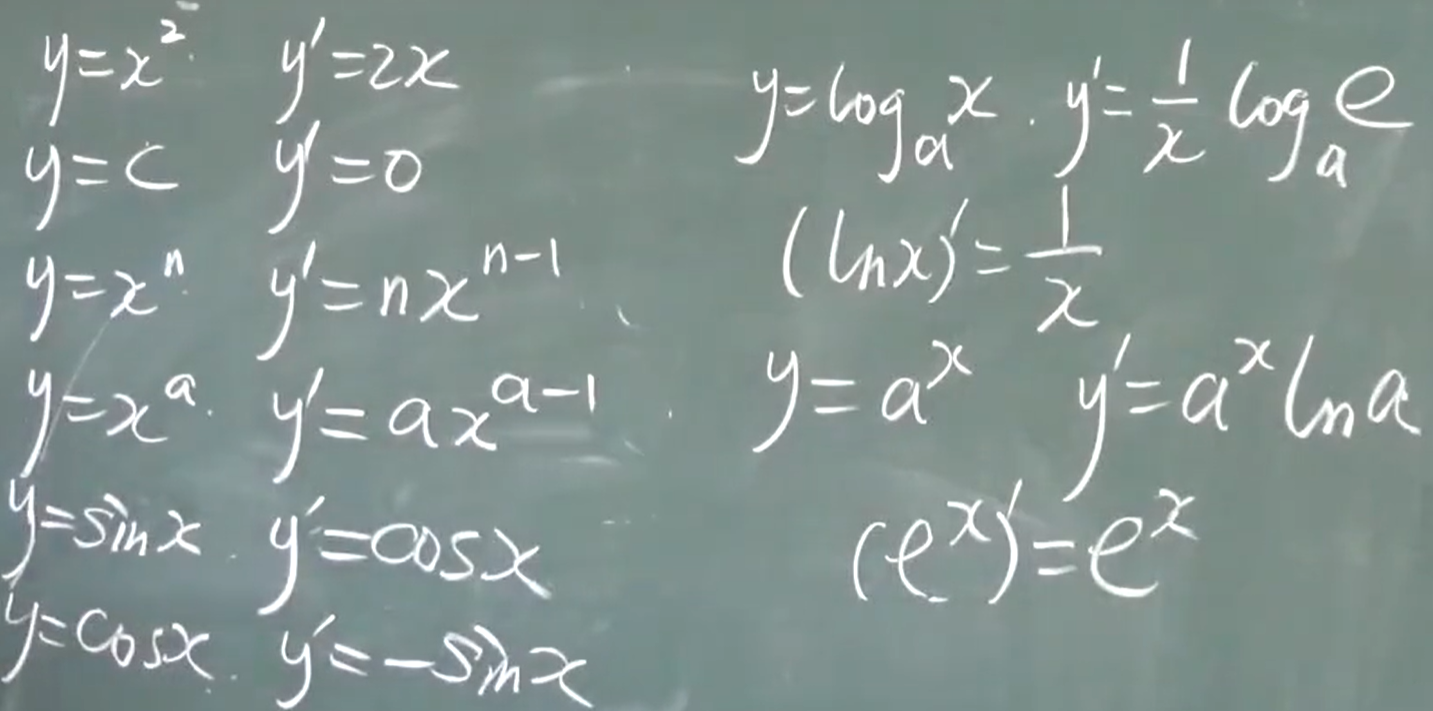
导数意义

例题：

求$y=x^3$在(1,1)的切线和法线

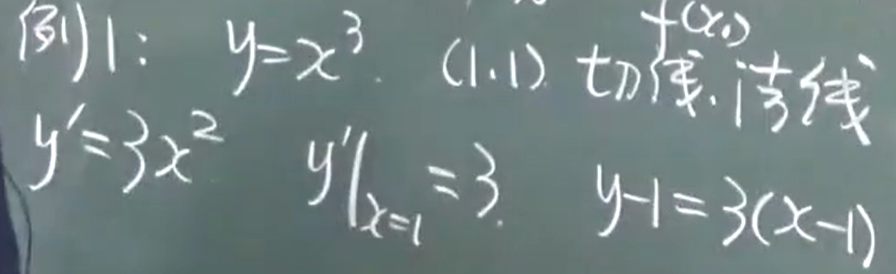
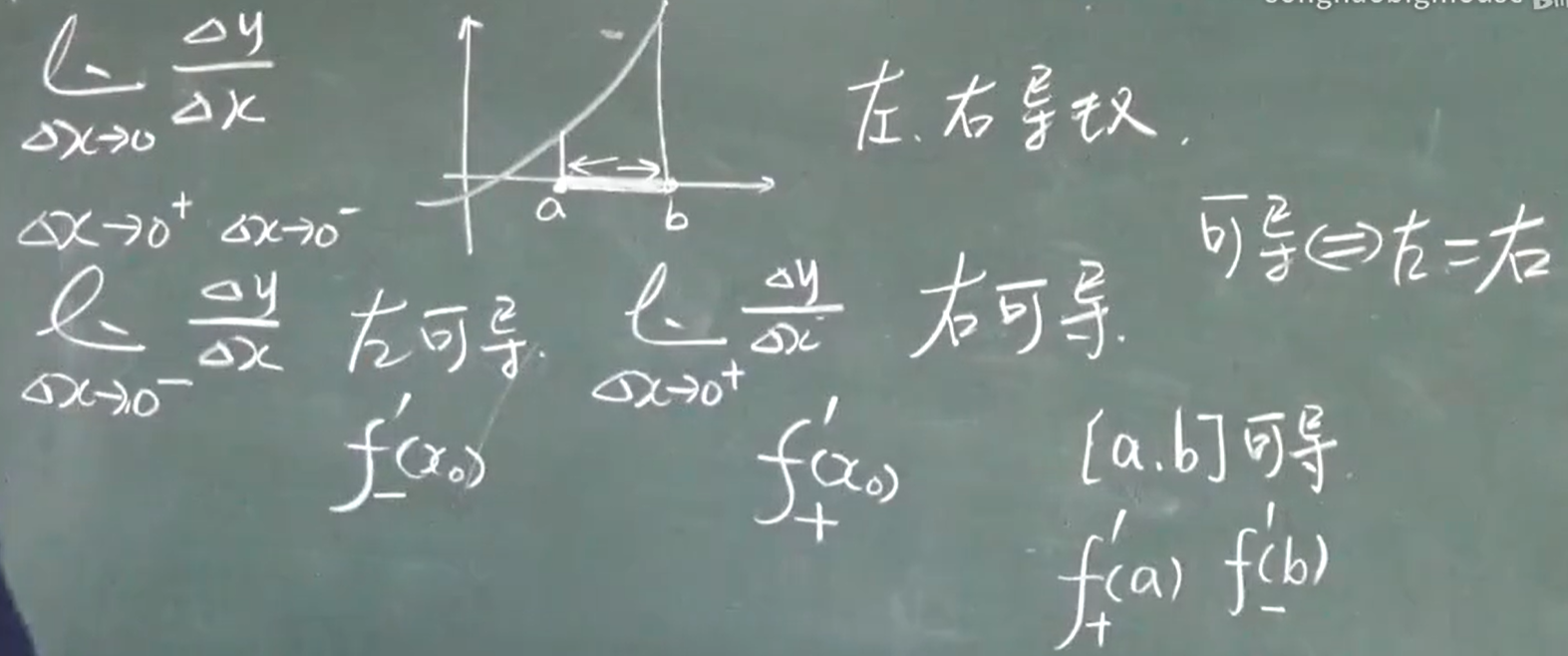
左右导数，左右导数都存在并相等

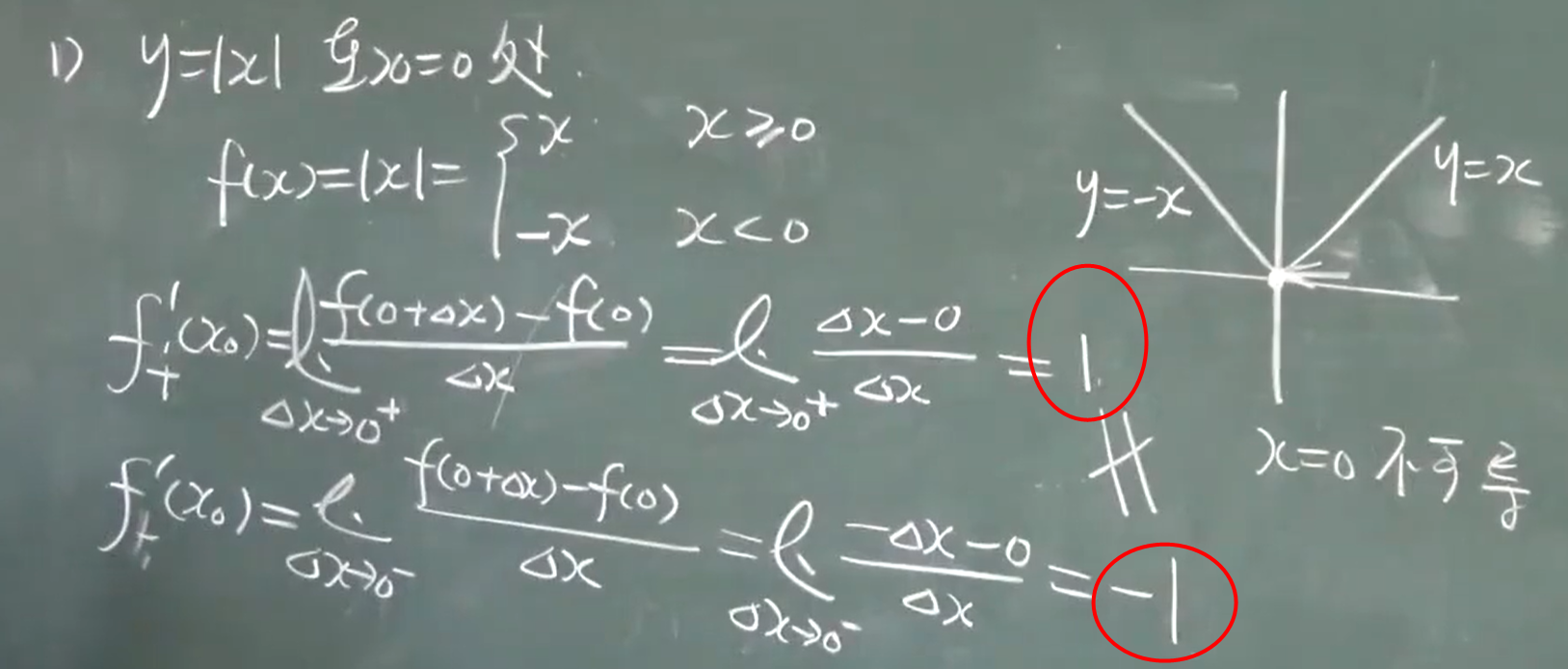
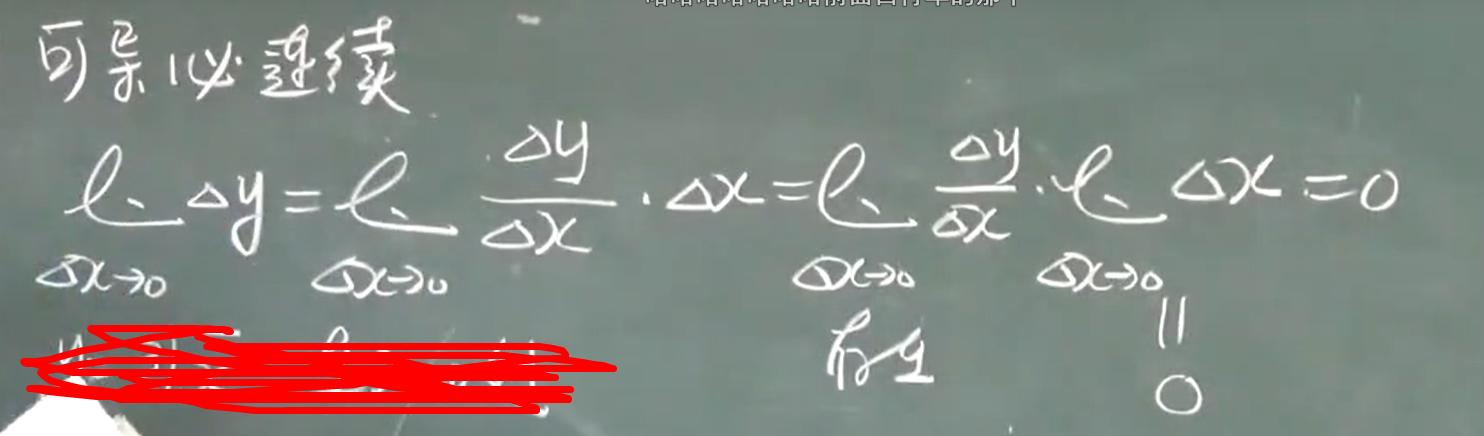
求导法则：

(1)$u(x)、v(x)$可导，$(u(x)+v(x))’=u’(x)+v’(x)$

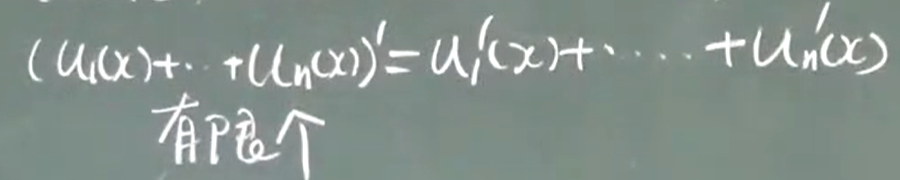
(2)$(uv)’=u’v+uv'$

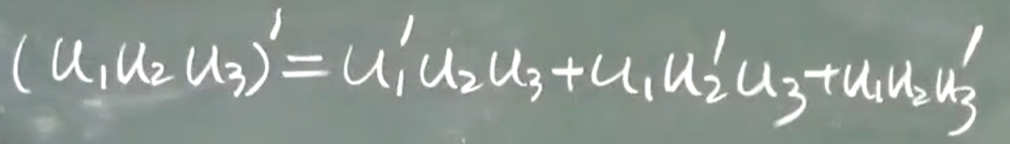
(3)$\frac{u}{v}=\frac{u’v+uv’}{v^2}$

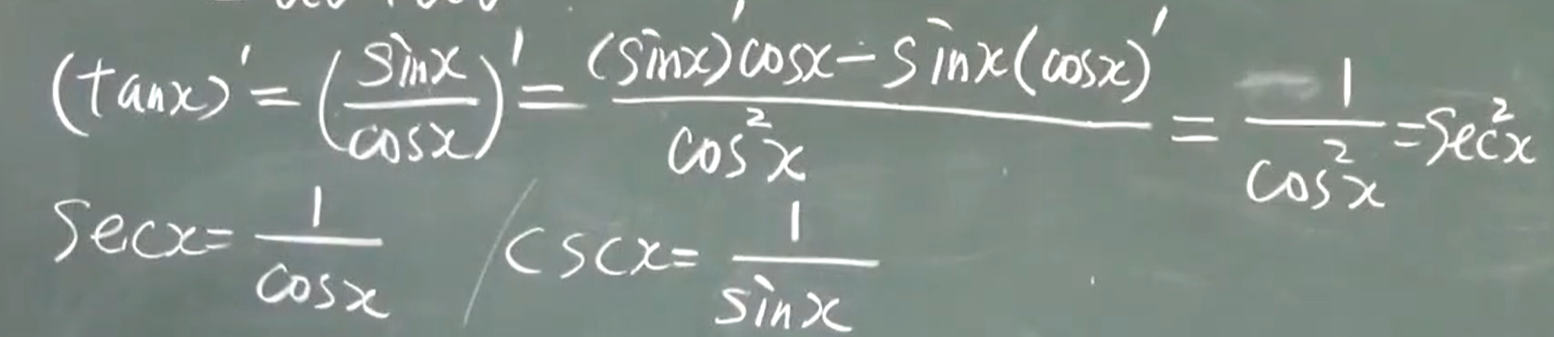
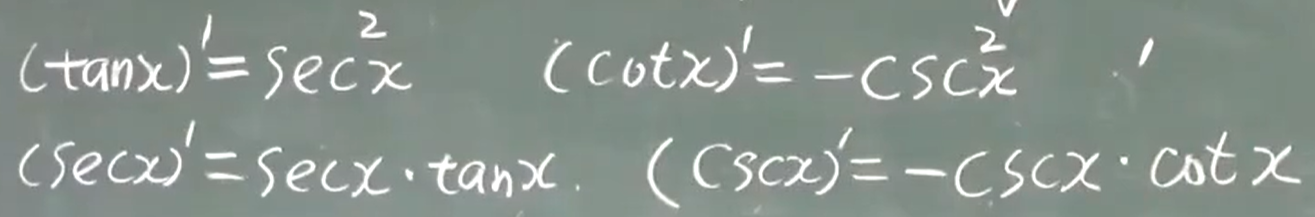
反函数求导法则：

$y=f(x)$ . $x=\phi(y)$

反函数=导数的倒数 $\phi(y)=\frac{1}{f’(x)}$

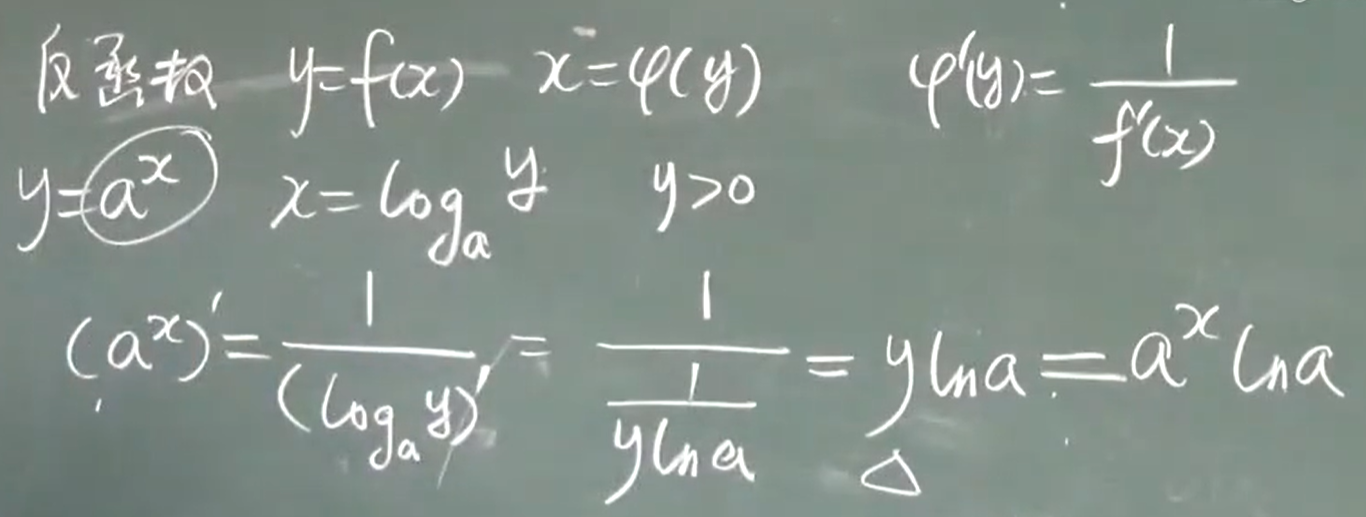
复合函数：

链式法则：

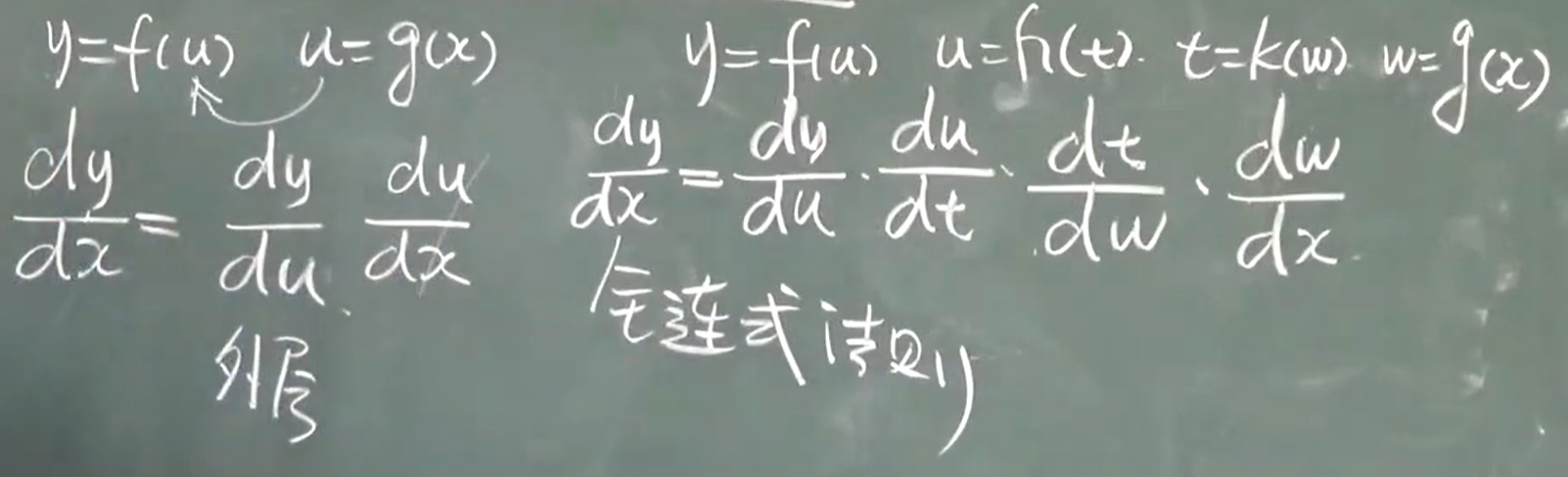
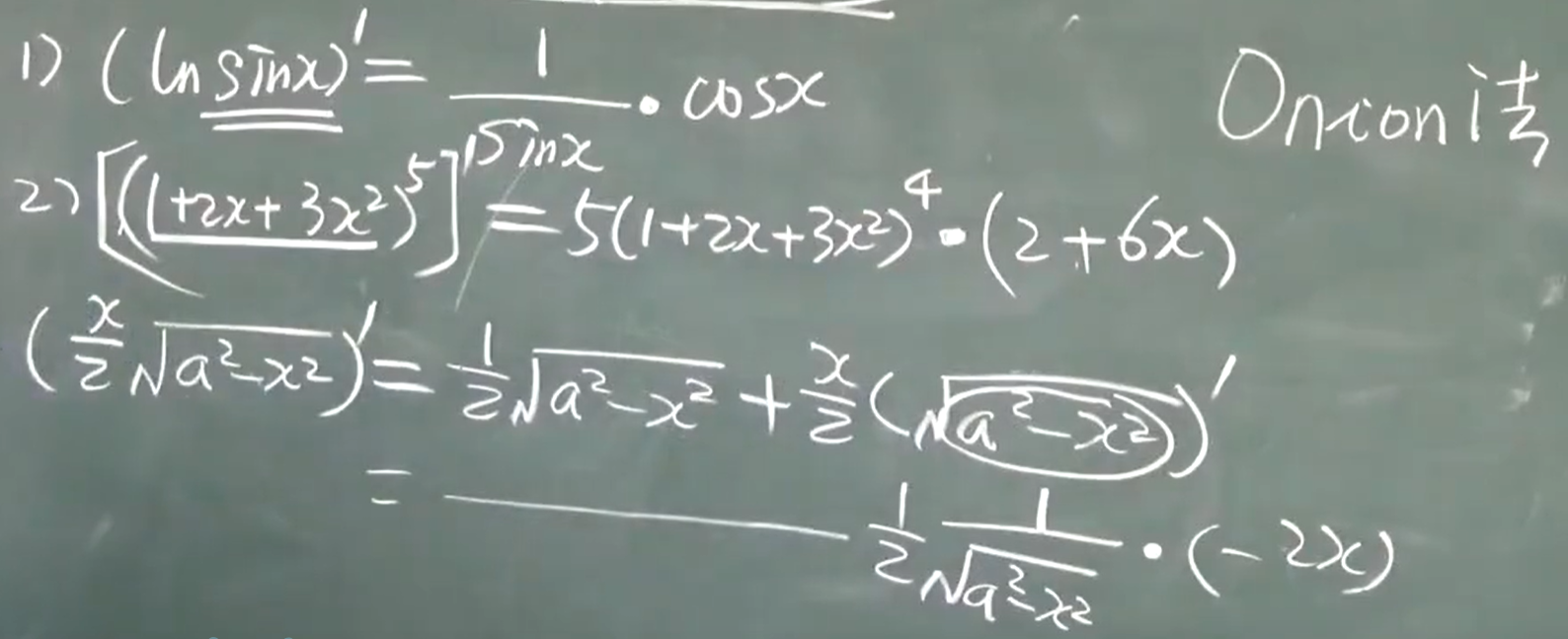
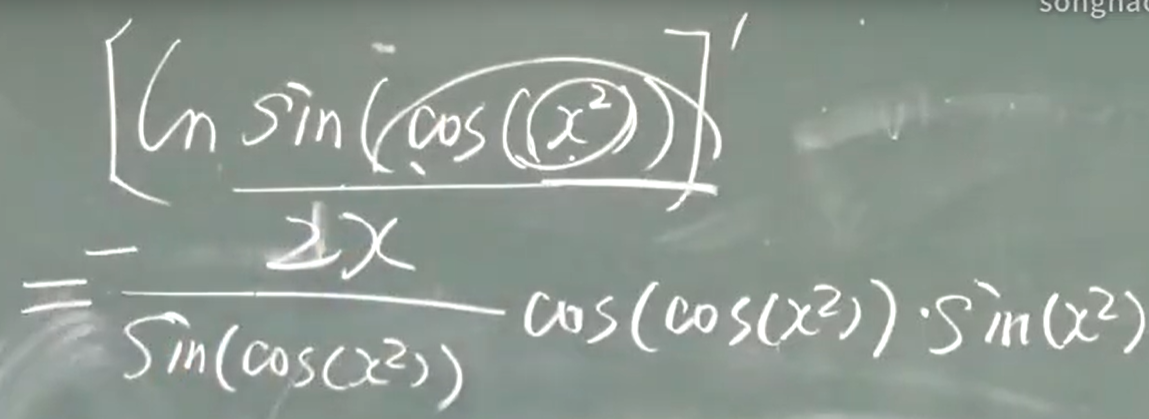
剥洋葱解法，从外往里剥。

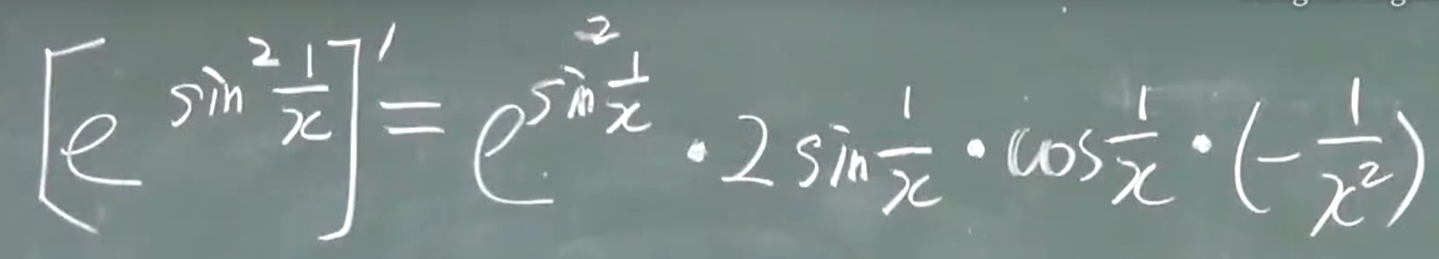
高阶函数

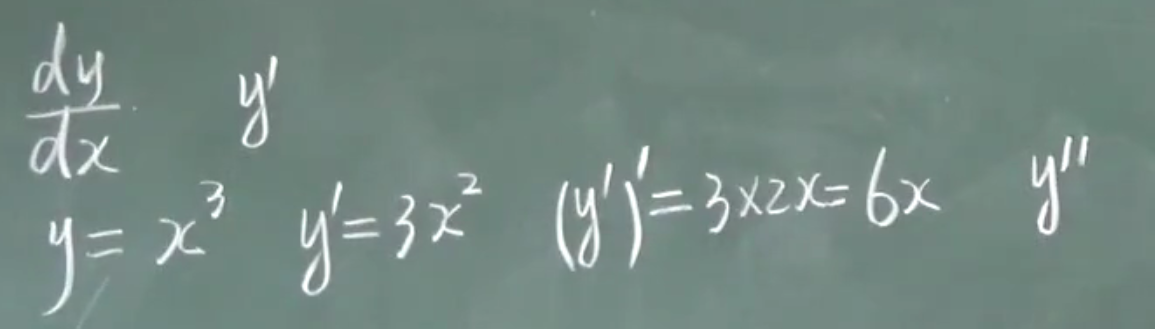
对$y$求两次导数，记作$y^{’’}$,二阶导数

或者$\frac{d^2y}{dx^2}$

从4阶开始用数字表示:$y^{(4)}$

例题：