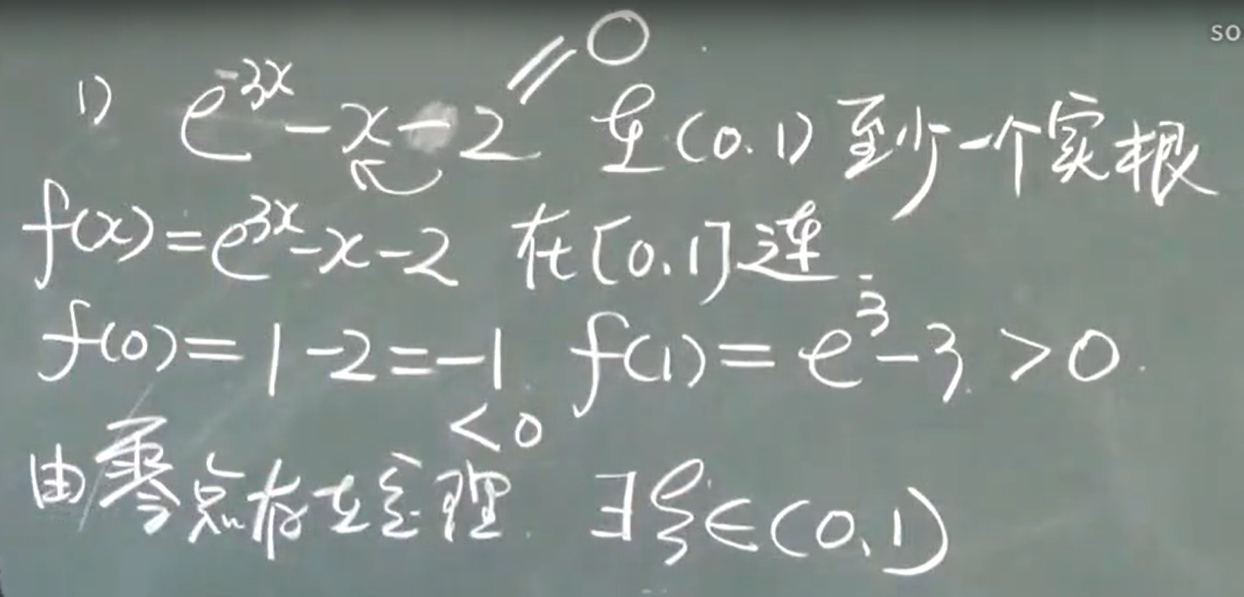增量(改变量)

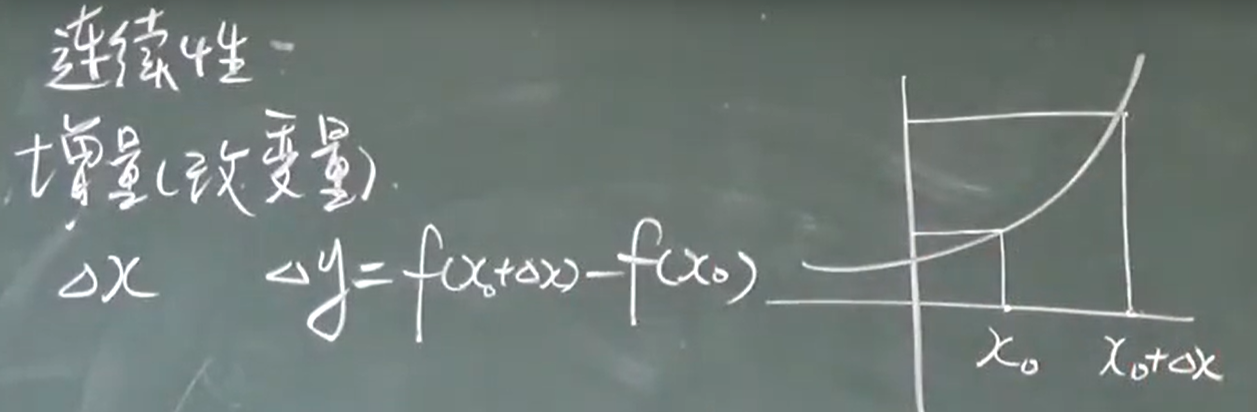
△x是自变量的增量，△y是因变量的增量

定义：

f(x)在$x_0$的邻域内有定义，$△x\to 0$,$△y\to 0$

$$\lim_{x\to 0}△y=\lim_{x\to 0} [f(x_0+△x)-f(x_0)]=0$$

&或者

$$\lim_{x\to x_0} f(x) = f(x_0)$$

那么就叫这个函数在这点$x_0$上是连续的

1)在$x_0$处有定义

2)$x\to x_0 f(x)$有极限

3)极限=在$x_0$处的定义，$f(x_0)$

左连续 $(x_0-\delta,x_0]$

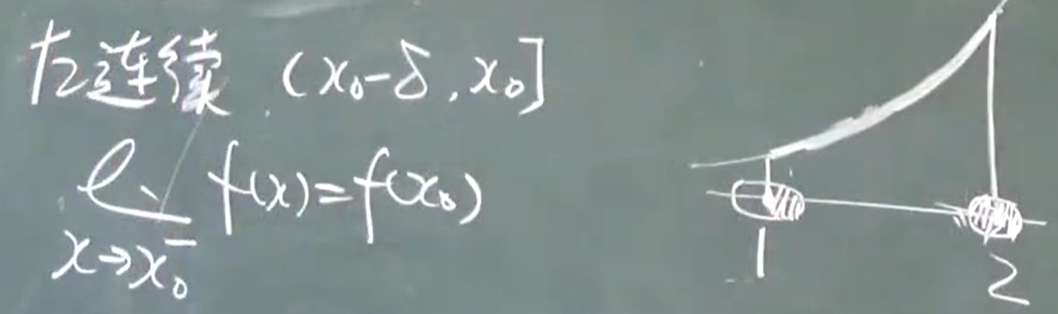
在x_0处连续的充要条件是既是左连续也是右连续

在区间上连续

间断点

连续的条件

1)在$x_0$处有定义

2)$x\to x_0 f(x)$有极限

3)极限=定义

• 无穷间断

  在$x_0$处没有定义

  

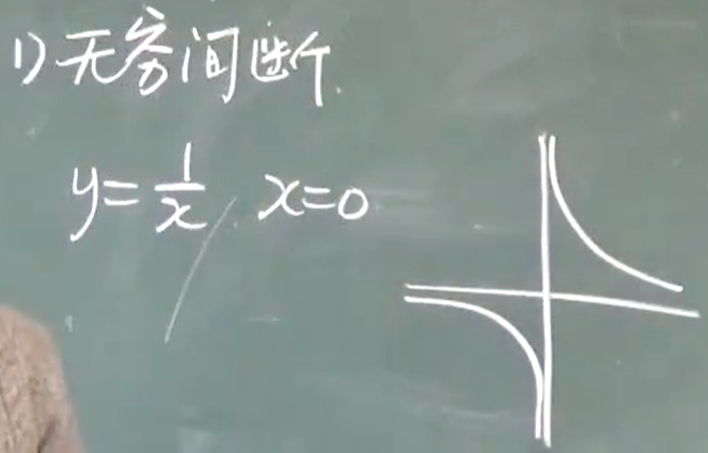
• 振荡

  $x\to x_0 f(x)$没有极限

  

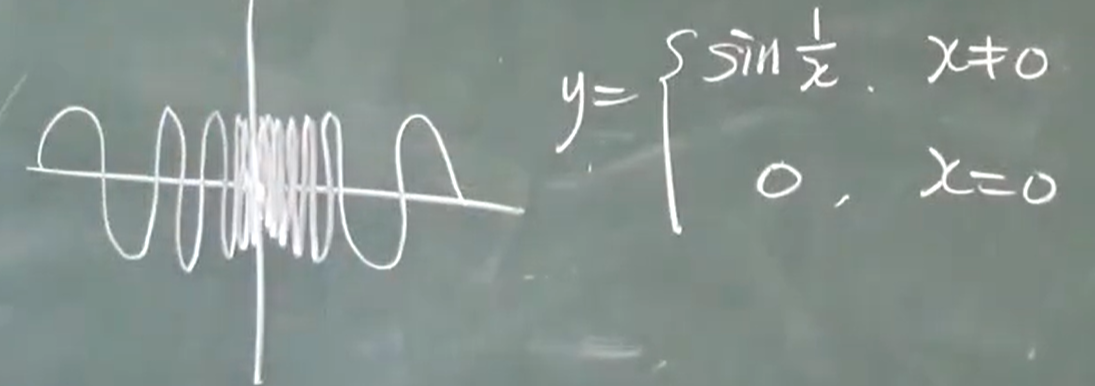
• 跳跃

  左右极限不相等

• 可去

  

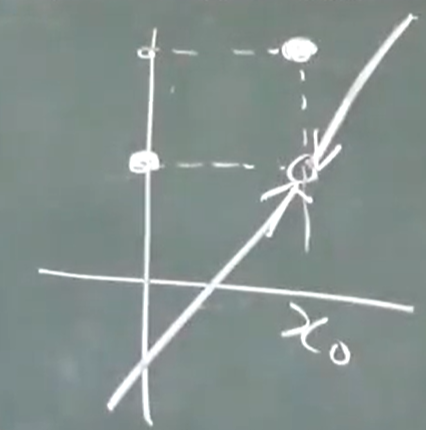
第一类间断点：

左右极限均存在，跳跃、可去间断点

第二类间断点：

左右极限不存在，无穷间断、振荡

例题：

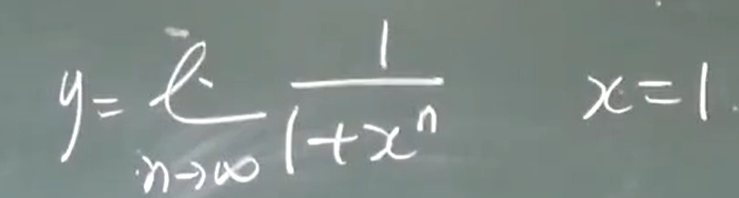
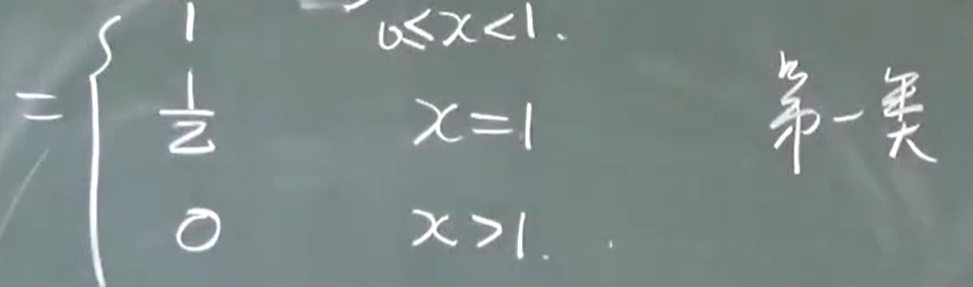
左右极限都存在但不相等

运算法则

四则运算 $f(x)±g(x).g(x)f(x).\frac{f(x)}{g(x)} (g(x)≠0)$ 依然连续

例题：

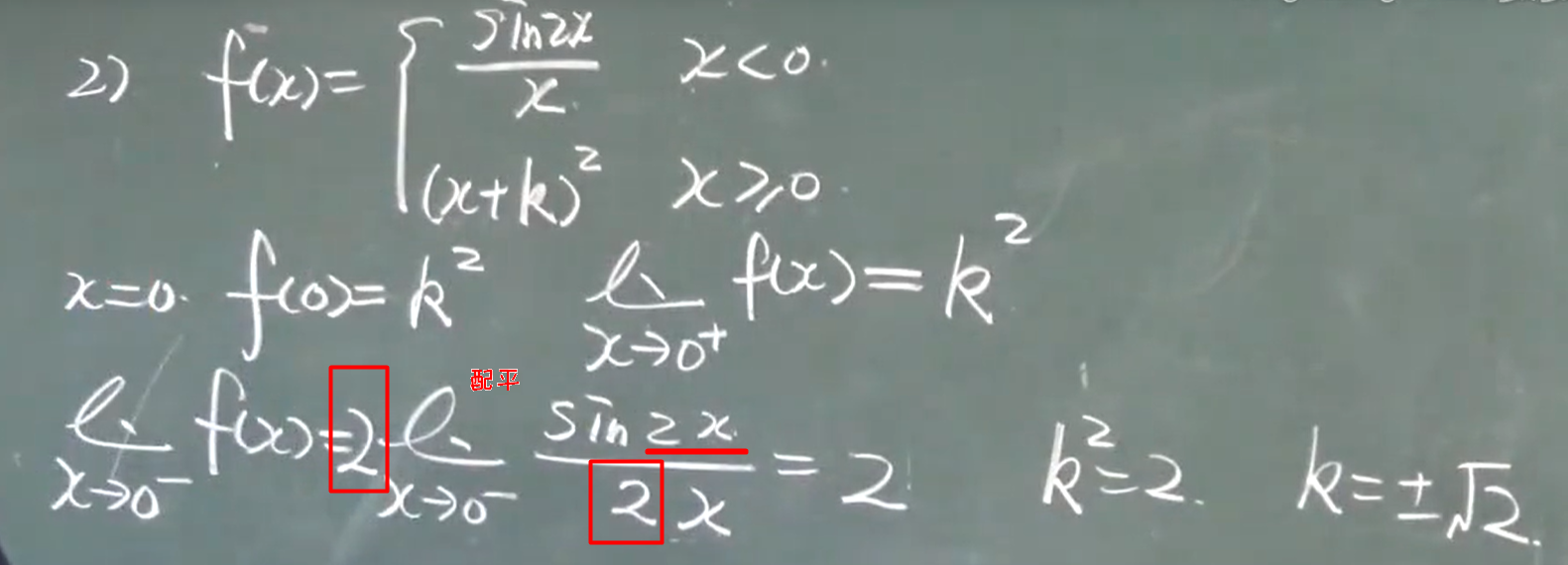
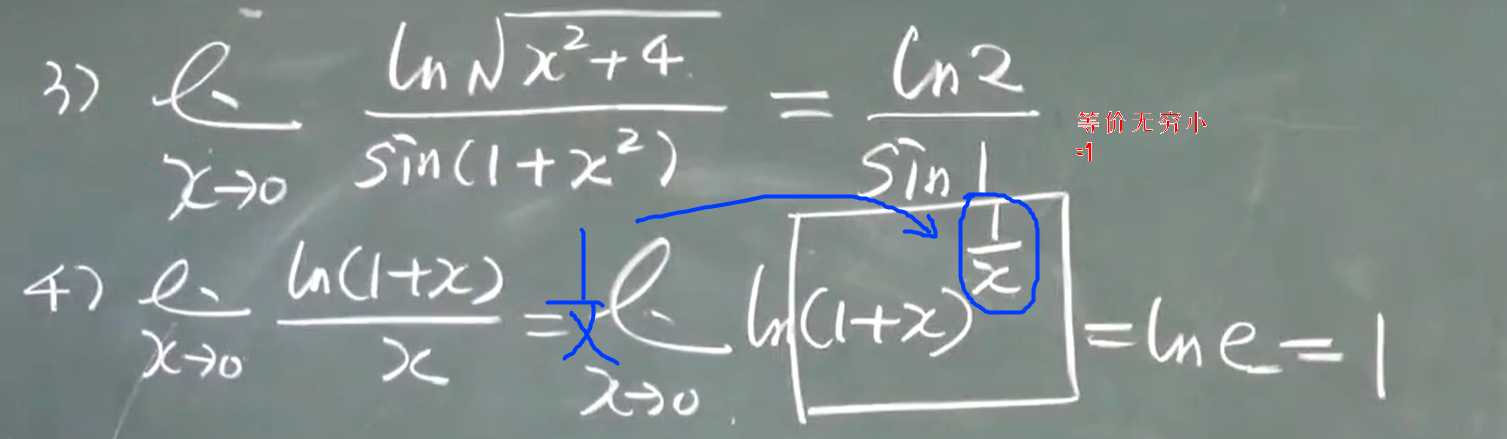
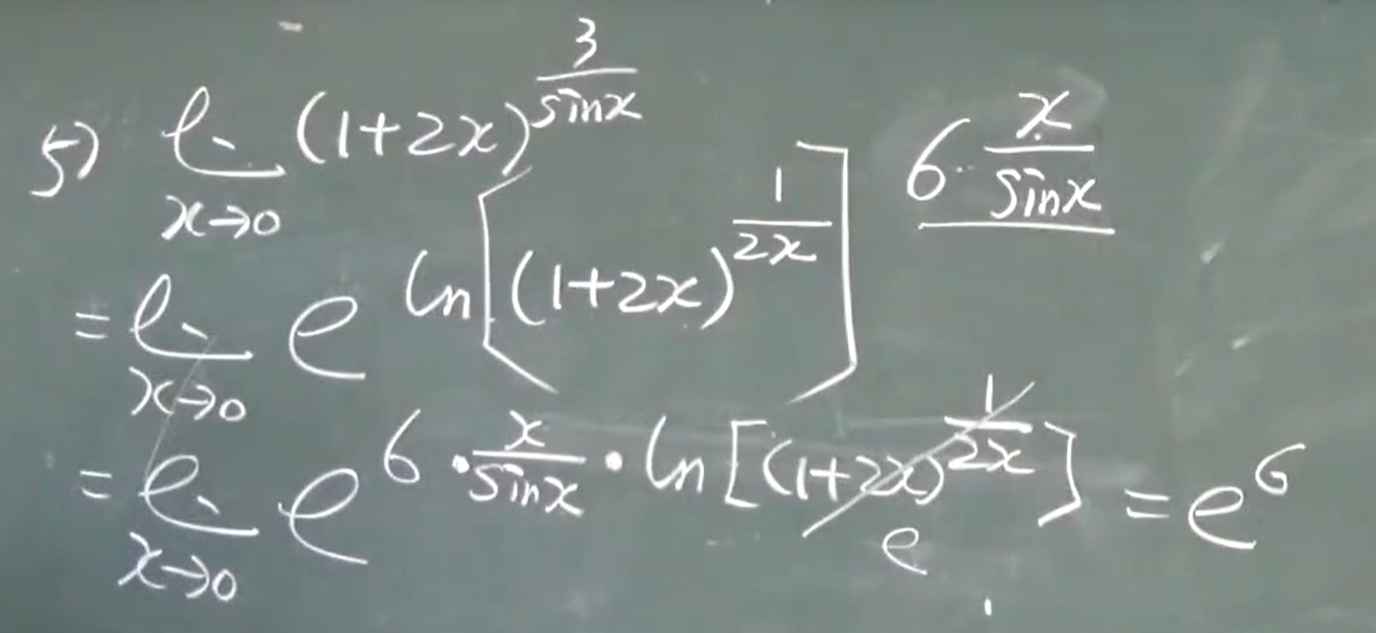
$f(x)= e^{lnf(x)}$、两个重要极限

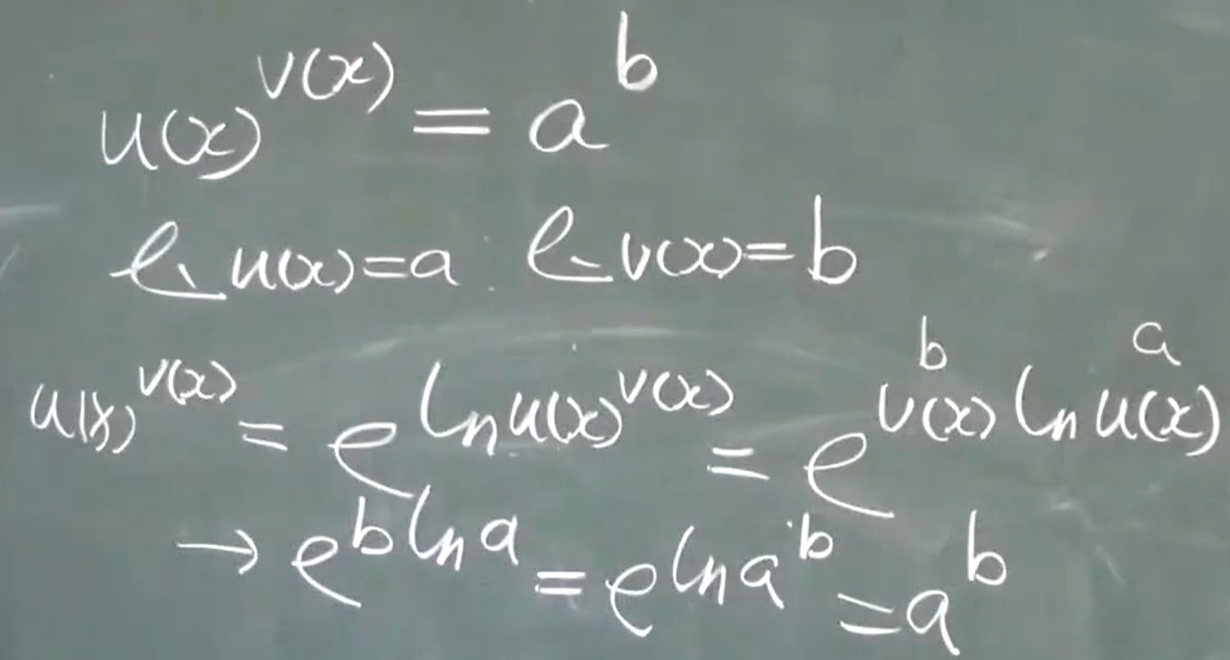
闭区间上连续性质

(有界性) 如果在$[a,b]$上是连续的，有界

(最值性) 如果在$[a,b]$上是连续的，b有最大最小值

(介值性) 如果在$[a,b]$上是连续的，最小值m，最大值M，介于m和M之间的任意一个取值：m<c<M

必存在一点$\xi$: $f(\xi)=c$

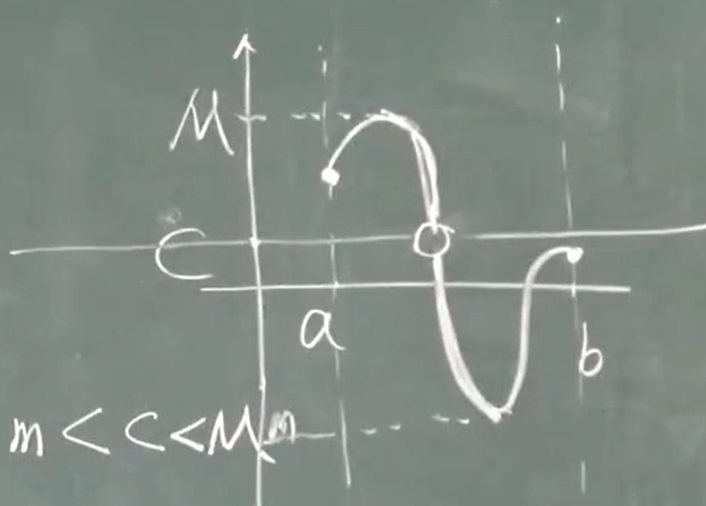
零点存在定理

[a,b]上是连续的，f(a)f(b)<0 异号

在(a,b)存在一点$\xi$，$f(\xi)=0$